The Two-dimensional Incompressible Gust

The simplest physically consistent theory is two-dimensional Sears’ theory assuming incompressible flow (see for instance Goldstein (1976)). Though it only addresses parallel gusts, it is presented for historical interest and because it already contains major physical features which will also be included in more sophisticated approaches. The local instantaneous lift fluctuation per unit span is distributed as:

where y = 2 yi/c is the non-dimensional chord-wise coordinate with refer­
ence at mid chord and k* = ki c/2 the non-dimensional aerodynamic wave number of the incident fluctuation in the chord-wise direction. The theory applies to a given wave number and requires a Fourier analysis of the in­cident fluctuations. S* is Sears’ function, expressed with Bessel functions as

2

S*(k*) = — ([Jc(k*) – Yi(k*)] – * [Ji(k*)+ Yo(k*)])-i.

П ki

Integrating eq. (2) along the chord line leads to the total unsteady lift force per unit span for the wave number k* of the incident gust

F(ki, t) = F(ki) в-іші = np0 cU0 W(k*) S*(k*) в-іші.

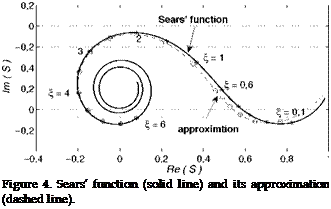
This result gives sense to the intuitively introduced transfer function T of section 2.2. Equation (2) shows that the lift fluctuations concentrate at the leading edge and decay to zero at the trailing edge. The center of action of the total fluctuating lift force is at the quarter-chord point. Sears’ function is plotted in Fig. 4. It does not depart so much from the approximation

The amplitude of Sears’ function decays as frequency increases. In that sense higher-frequency fluctuations correspond to lower aerodynamic effi­ciency.

Assuming incompressibility means that the sound speed is considered infinite in view of the time and velocity scales involved in the aerodynamic processes. This is acceptable if the time taken for the airfoil response to in­cident disturbances remains much smaller than the periods of oscillations. If the response to an event occurring at the leading edge involves transmission of information down to the trailing edge plus back-transmission upstream to the leading edge accounting for the effect of the Kutta condition, the condition reads

with в2 = 1 — M2, Mq = Uq/cq. In other words, since Aa = 2n/k1,

Mokt kc n

——— = ——- – C —

в 2 в2 2

The incompressible Sears and von Karman’s solution is therefore only valid if the chord is compact and if the Mach number is sufficiently small. As a result the effect of compressibility is important not only at high Mach number but also at high frequencies (Homicz & George (1974)). In many cases of interest the aforementioned condition is not fulfilled and a com­pressible solution is needed.