THEORIES OF TAIL BUFFETING
The similarity of the wake behind a stalled airfoil and that behind a circular cylinder suggests at once a “vortex-shedding” theory of tail buffeting. In Abdrashitov’s analysis91 the wing wake is regarded as a well developed vortex street in which the vortices are regularly spaced, and the buffeting motion of the tail is computed as a forced vibration. The random characteristics of tail buffeting are neglected.
A different idealization is made by Shih-chun Lo9’12 who regards the wing wake as a vortex sheet—an “interface” without thickness, across which the flow undergoes a sudden change in velocity and density. Velocity potential is assumed to exist on both sides of the interface. It is shown that the vortex sheet reacts strongly with an oscillating airfoil located in the neighborhood of the interface, particularly for higher values of the reduced frequency. Large reduction of flutter speed, due to the presence of an interface, is indicated. It is impossible to verify experimentally Lo’s mathematical theory, because such an idealized interface cannot be produced. However, wind-tunnel tests made by Dankworth and Walker,9-6 using a “barrier” which blocks partly the flow in the working section, do not indicate any significant change in flutter speed of an airfoil when the distance between the airfoil and the “interface” (which is taken as the tangent to the barrier) exceeds 20 per cent of the chord length of the airfoil. When this distance is less than 20 per cent of the chord length, irregular motion of the airfoil is observed which is clearly due to turbulences in the jet mixing region.
Liepmann911 points out that buffeting is the response of an elastic body to a turbulent flow, and hence is a stochastic process. A correct theory of buffeting, therefore, must account for the turbulent characteristics of the oncoming flow. If the power spectrum of the turbulences in the flow is known, the intensity of the buffeting motion can be calculated in a
manner similar to the gust-response calculation of the previous chapter, provided that the intensity of turbulence is so low and the amplitude of the wing motion is so small that the wing is never stalled during buffeting. If stalling did occur, even only for a fraction of the time, the relation among the lift, the turbulent fluctuations, and the wing motion becomes nonlinear, and the calculation of the buffeting intensity is more difficult. We must point out that, turbulence being a stochastic process, large – velocity fluctuation may exist, though infrequently, even if the root mean square of the velocity fluctuation is small. Hence the chance of the wing’s being stalled always exists.
One feature of the flow in the wake of a stalled wing seems undisputed. As with flow in the wake of a circular cylinder (see § 2.3), there may exist one or more frequencies at which the power spectrum has sharp peaks. These “predominant” frequencies are those at which the kinetic energy of the turbulent motion is more or less concentrated. Experimental values of the predominant frequency in the wake behind flat plates and airfoils in incompressible fluids are given by Page and Johansen;9-39 Tyler;9,40 Blenk, Fuchs, and Liebers;9,36 and Dunn and Finston.9,38 All agree that, for angles of attack above about 30°, the reduced frequency, at the predominant peak of the power spectrum, is nearly a constant, independent of the angle of attack, provided that the projected length of the chord normal to the direction of flow is taken as the characteristic length. If the chord length is c and the angle of attack is oc, the projected length is c sin a. The reduced frequency that remains constant is nc sin a/ U, where n is the wave number (cycles per second) of the vortices, and U is the mean speed of flow. There are numerical discrepancies between various authors as shown in Table 9.1.
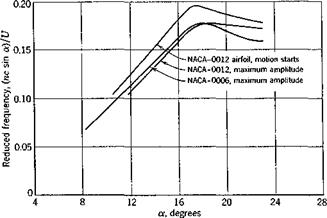
For smaller angles of attack, the variations of the values of the reduced frequency nc sin ct/U given by various authors become large, and seem strongly affected by the Reynolds number.* For angles of attack near and below the stalling angle, the reduced frequency nc sin a/17 decreases. The results of Dunn and Finston9,38 are shown in Fig. 9.5. Tyler’s result is similar, but the absolute values are smaller, whereas Blenk’s result shows very little decrease in the reduced frequency nc sin a/U for a down to 10°.
It may be noticed that the results as shown in Fig. 9.5 suggest that, for angles of attack a less than about 17°, the predominant vortex frequency is nearly proportional to a. Hence, a reduced frequency based on the chord length itself, ncjU, will remain nearly a constant. The average value of ncjU, for a between 8 to 17°, is approximately 0.54.
* See Chuan and Magnus.9,21 The reduced frequency nc sin a/U increases from 0.112 at R = 9.3 x 101 to 0.178 at 7? = 21 x 104, in the range of a between 18 and 29°.
|
Fig. 9.5. The variation of the reduced frequency {nc sin oc)/I/ with angle of attack a. Measurements by Dunn and Finston, Ref. 9.38. Reynolds number 6 x 104 to 24 x 104. |
(a) For Flat Plate
|
Table 9.1 The Predominant Vortex Frequency in the Wake of Flat Plates and Airfoils
|
|
(6) For Airfoils
|
It may also be noted that the value of nc sin ocjU in Fig. 9.5, when multiplied by 277, give values of reduced frequency of comparable magnitude to those shown in Fig. 2.4 for the wake of a circular cylinder.