Wave Tracing

These ideas of source time and arrival time of sound waves are formally embodied in a process known as wave tracing. In a fixed reference frame with respect to the rotor the spherical wavelets that propagate radially from each source point proceed at the local speed of sound plus the component of the flow velocity in the propagation direction, that is, say initially in a direction /3 relative to the blade. For example, for an outward moving source point the initial wavelet trajectory over a period At can be formalized as

(8.248)

where (jcв, Ув, Zb) is the acoustic source point on the blade, fa is the blade azimuth angle (or time) of the acoustic source point and (u, v,w) can be considered as the local flow velocities relative to a coordinate system at the rotor hub.

For illustration, it is useful to consider a model problem of the sound field radiated by a rotating point source that has a subsonic Mach number, which is typical of the helicopter rotor. This is a simple problem in concept, but is complicated even here. The principles involved, however, contain most of the physics associated with the acoustics of real rotors. Assume that an acoustic source at a given radius rotates at frequency ft, as shown previously in Fig. 8.44. Assume first that there is no forward motion of the source and no relative flow velocity, so this system corresponds to a helicopter rotor in hover. The results in Fig. 8.46(a) show that the wave fronts coalesce along a spiral and move away from the source point at the speed of sound. With forward speed of the source, in this case with a relative flow from left to right, Fig. 8.46(b) shows that the wave fronts propagate at the speed of sound plus or minus the local flow velocity. In this case upstream moving waves bunch closer together and the downstream moving waves are spread further apart. This is essentially a

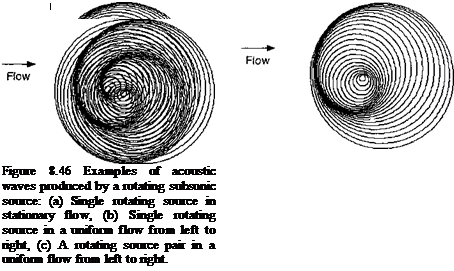Doppler effect, which manifests as an increase or decrease of the apparent sound frequency and intensity at upstream or downstream observer locations, respectively. The addition of a second source, as shown in Fig. 8.46(c), makes the problem much more complicated. With the many different potential sound sources on a helicopter rotor, the net sound field tends to be very omnidirectional, but with embedded regions of focused noise.