Wings in compressible flow

In this section the compressible-flow equations in their various forms are considered in order to predict the behaviour of aerofoil sections in high sub – and supersonic flows. Except in the descriptive portions the effects of viscosity are largely neglected.

6.8.1 Transonic flow, the critical Mach number

When the air flows past a body, or vice versa, e. g. a symmetrical aerofoil section at low incidence, the local airspeed adjacent to the surface just outside the boundary layer is higher or lower than the free-stream speed depending on whether the local static pressure is less or greater than the ambient. In such a situation the value of the velocity somewhere on the aerofoil exceeds that of the free stream. Thus as the free- stream flow speed rises the Mach number at a point somewhere adjacent to the

surface reaches sonic conditions before the free stream. This point is usually the minimum-pressure point which in this case is on the upper surface. The value of the free-stream Mach number (Moo) at which the flow somewhere on the surface first reaches M = 1 is called the critical Mach number, Mc. Typically for a slender wing section at low incidence Mc may be about 0.75. Below that critical Mach number the flow is subsonic throughout.

Above the critical Mach number the flow is mixed, part supersonic part subsonic. As Moo is increased progressively from low numbers to Mc the aerodynamic char­acteristics of the aerofoil section undergo progressive and generally smooth changes, and for thin aerofoil shapes at low incidences these changes may be predicted by the small-perturbation or linearized theory outlined below due to Prandtl and Glauert.

As Moo is increased progressively beyond Mc a limited region in which the flow is supersonic develops from the point where the flow first became sonic and grows outwards and downstream, terminating in a shock wave that is at first approximately normal to the surface. As ¥„ increases the shock wave becomes stronger, longer and moves rearwards. At some stage, at a value of Mx > Mc, the velocity somewhere on the lower surface approaches and passes the sonic value, a supersonic region termin­ating in a shock wave appears on the lower surface, and that too grows stronger and moves back as the lower supersonic region increases.

Eventually at a value of Мж close to unity the upper and lower shock waves reach the trailing edge. In their rearward movement the shock waves approach the trailing edge in general at different rates, the lower typically starting later and ahead of the upper, but moving more rapidly and overtaking the upper before they reach the trailing edge. When the free-stream Mach number has reached unity a bow shock wave appears at a small stand-off distance from the rounded leading edge. For higher Mach numbers the extremes of the bow and trailing waves incline rearwards to approach the Mach angle. For round-nosed aerofoils or bodies the bow wave is a ‘strong’ wave and always stands off, and a small subsonic region exists around the front stagnation point. The sequence is shown in Fig. 6.31. For sharp leading edges the bow shock waves are plane, and usually ‘weak’, with the downstream flow still, at a lower Mach number, supersonic. This case is dealt with separately below.

The effect on the aerofoil characteristics of the flow sequence described above is dramatic. The sudden loss of lift, increase in drag and rapid movement in centre of pressure are similar in flight to those experienced at the stall and this flight regime became known as the shock stall. Many of the effects can be minimized or delayed by design methods that are beyond the scope of the present volume.

To appreciate why the aerofoil characteristics begin to change so dramatically we must recall the properties of shock waves the first appearance of which signals the start of the change. Across the shock wave, which is the only mechanism for a finite pressure increase in supersonic flow, the pressure rise is large and sudden. Moreover the shock wave is a process accompanied by an entropy change which manifests itself as an immediate rise in drag, i. e. an irreversible conversion of mechanical energy to heat (which is dissipated) takes place and sustaining this loss results in the drag. The drag increase is directly related to the strengths of the shock waves which in turn depend on the magnitude of the supersonic regions ahead. Another contribution to the drag will occur if the boundary layer at the foot of the shock separates as a consequence of accommodating the sudden pressure rise.

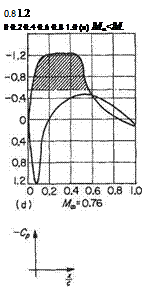
The lift on the other hand continues to rise smoothly with increase in Mx > Mc as a consequence of the increased low-pressure area on the upper surface. The sequence is seen in Fig. 6.32. The lift does not begin to decrease significantly until the low-pressure area on the lower surface becomes appreciably extensive owing to the

growth of the supersonic region there; Fig. 6.32c. The presence of the shock wave can be seen by the sharp vertical pressure recovery terminating the supersonic regions (shaded areas in Fig. 6.32). It is apparent that the marked effect on the lift is associated more with the growth of the shock wave on the lower surface. Movement of the centre of pressure also follows as a consequence of the varying pressure distributions and is particularly marked as the lower shock wave moves behind the upper at the higher Mach numbers approaching unity.

It may also be noted from the pressure distributions (e) and (f) that the pressure recovery at the trailing edge is incomplete. This is due to the flow separation at the feet of the shock waves. This will lead to buffeting of any control surface near the trailing edge. It is also worth noting that even if the flow remained attached the pressure information that needs to be propagated to the pressure distribution by a control movement (say) cannot be propagated upstream through the supersonic region so that the effectiveness of a trailing-edge control surface is much reduced. As the free-stream Mach number Mx becomes supersonic the flow over the aerofoil,

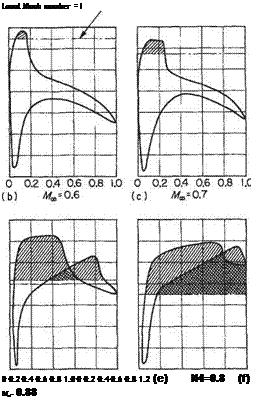Fig.6.32 Pressure distribution on two-dimensional aerofoil (Mait = 0.57) as Mx increases through Mait

except for the small region near the stagnation point, is supersonic, and the shock system stabilizes to a form similar to the supersonic case shown last in Fig. 6.31.