. Effective Diffusivity

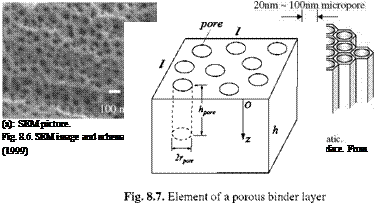
Diffusion in a porous material can be considered as a diffusion problem in a two – phase system made up of one disperse phase and one continuous polymer or other material. In PSP, the disperse phase is composed of numerous pores filled with air. Figure 8.6 shows a typical scanning electron microscopic (SEM) image of an anodized aluminum (AA) surface for PSP. Consider an element of a porous polymer layer of the length l, width l, and thickness h, as shown in Fig. 8.7. The coordinate z is normally directed to the polymer layer from the upper surface of the layer. First, we assume that many cylindrical (tube-like) pores are distributed and oriented in the z-direction in the element. The effective radius and depth of a pore are denoted by rpore and hpore, respectively. The radius of a pore is much larger than the size of a molecule of oxygen. In general, the depth of a pore is smaller than or equal to the layer thickness, i. e., hpore < h. For simplicity of

expression, the normal directional derivative of the oxygen concentration [O2 ] at

The effective diffusivity Dmeff of the porous polymer layer with many

cylindrical pores is given by a balance equation between the mass transfer through the apparent homogenous upper surface and the total mass transfer across the air – polymer interface, i. e.,

where Npore is the total number of the pores in the element and Dm is the

diffusivity of the polymer continuum. The integral term in Eq. (8.21) is the total mass transfer across the peripheral surface of the pores in the element. Thus, the effective diffusivity Dmeff is given by

1 + [vn( hpore )/Vn(0) – 1]Npore П r2pore l~2 -2 —1 Г hpore

+ Npore 2n rpore l~vn(0)]0 Vn(z)dz

In a simplified case where vn(z) = const. across the thin layer, Eq. (8.22) becomes

Dmeff / Dm = 1 + 2 av rpore h, (8.23)

where av = Npore nr2pon hpore l~2h – is the volume fraction of the cylindrical pores

in the polymer layer. Eq. (8.23) indicates that an increase of the effective diffusivity is proportional to the volume fraction of the pores and a ratio between the polymer layer thickness and the radius of the pore. Eq. (8.23) for Dmeff is

valid only for an ideal porous polymer layer with the straight cylindrical pores oriented normally. Nevertheless, this model can be generalized for real porous polymers where topology of the pores is often highly complicated.

For more realistic modeling, the topological structure of a pore is considered as a highly convoluted and folded tube in a polymer layer while the cross-section of the tube remains unchanged. The integral in Eq. (8.22) should be replaced by an integral along the path of a highly convoluted tube-like pore. In this case, the concept of the fractal dimension should be introduced because the length of a highly convoluted tube is no longer proportional to the linear length scale of the tube in the z-direction (e. g. hpore) (Mandelbrot 1982). According to the length-

area relation for a fractal path, the integral along the path is proportional to Af2

or hf, where dfr (1 < dfr < 2 ) is the fractal dimension of the path of a pore

and Apore <x h2pore is the characteristic area covering over the path. Loosely

speaking, the fractal dimension represents the degree of complexity of the pore pathway. In order to take the fractal nature of pores into account, Eq. (8.22) is generalized using a Riemann-Liouville fractional integral of the order dfr, i. e., (Nishimoto 1991)

Dmeff /Dm = 1 + [vn( hpore )/vn(0) _ 1 ]Npore П rtIre l~2

, Chpore d. (8.24)

+ Npore2nrporel v_1(0) vn(z)(dz) fr

Note that a unitary constant with the dimension [m1_dfr ] is implicitly embedded in the third term in the right-hand side of Eq. (8.24) to make Eq. (8.24) dimensionally consistent. This dimensional constant is implicitly contained in all the results derived from Eq. (8.24). In a simplified case where vn(z) = const. across a thin layer, a generalized expression for Dmeff is

where Г( 1 + d fr ) is the gamma function. Here, hpore is interpreted as a linear length scale of a convoluted tube in the z-direction and av is the volume fraction
of the apparent cylindrical pores. Eq. (8.25) clearly shows that the effective diffusivity Dmeff is not only proportional to hdfr, but also related to the porosity parameters aV rp0re and hpore /h. For dfr = 1, Eq. (8.25) is simply reduced to Eq. (8.23) for the straight cylindrical pores.