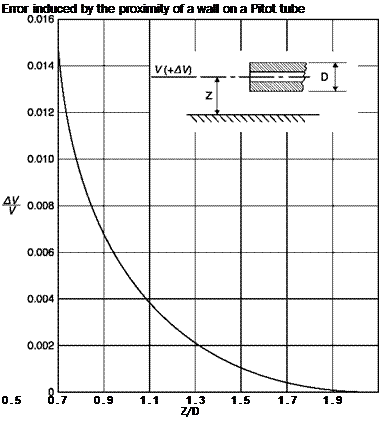
Effects of the Mach number
For a probe perfectly aligned with the stream, the reading is independent of the Mach number up to Mach numbers close to 1 (Figure 2.10). At supersonic speeds in front of the tube, a detached shock wave is generated, which is locally normal to the axis of the tube, so that the pressure detected by the Pitot tube is the stagnation pressure downstream of a
normal shock wave. The measured pressure (subscript 2) can be used to calculate the Mach number of the stream (M1 > 1), if the stagnation pressure upstream of the shock wave (subscript 1) is known, through the equation, known as the Rayleigh formula:
Y 1
![]()
![]()
 |
(Y – 1)Mi + 2 Y-1 ( 2y M2 – Y-1 Y-1
(y + 1)Mj2 lr +1 1 Y + 1J
The stagnation pressure upstream of the shock wave must be measured independently, as the pressure in the stagnation chamber that feeds the de Laval nozzle that generated the supersonic stream.
The Mach number can also be calculated, if the static pressure upstream
![]()
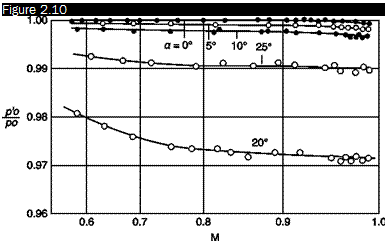 |
Effects of the Mach number on the readings of a Pitot tube with a hemispherical head (d/D = 0.3)
of the shock wave is known, by Equation (2.6) obtained by dividing Equation (2.5) by Equation (2.1):
Y 1
![]()
![]() ___ 2___ Y-1 (JY_ M2 _ Y-1Y-1
___ 2___ Y-1 (JY_ M2 _ Y-1Y-1
(y + 1)M Iy + 1 Y + 1)
The static pressure upstream of the shock wave can be measured on a wall at the entrance of the test chamber.













