Einfache Traglinientheorie

7.331 Grundgleichung. Die Grundgleichung fur die Prandtlsche Traglinientheorie wurde in Gl. (7.10) bereitgestellt:

* (У) = «Є (У) + <*І (у), (7.64)

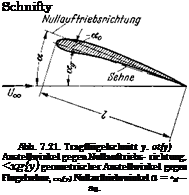
wobei jetzt ос (у) nach Abb. 7.21 der Anstellwinkel gegeniiber der Null – auftriebsrichtung ist.

Fiihrt man die folgenden dimensionslosen Werte ein:1

V = %■ = *-. (7.65.)

0 s

= (7.65b)

9h

fW = 7h> <7-65c)

С’аоо*’

so wird nach Gl. (7.11) fur den effek – tiven Anstellwinkel

«6(»?)=/(»?) Y(n) (7-66)

und nach Gl. (7.12) fur den induzier – ten Anstellwinkel2

1

1 Г dy dr]’

2 л J dr]’ r] — rj’

-l

Es moge f(r]) als GrundrififunJction bezeichnet werden.

Setzt man die beiden letzten Gleichungen in Gl. (7.64) ein, so erhalt man die Prandtlsche Integralgleichung fur die dimensionslose Zir-

1 Gegeniiber Кар. 7.1 wird die Anstromgesehwindigkeit statt mit V jetzt mit Uoo bezeichnet.

2 Die Formel fiir <%,■ [r]) kann nach partieller Integration auch wie folgt geschrie – ben werden:

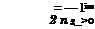1 rto) – l

fi J (у — Ч Г

. – l

3 Schlichting/Truckenbrodt, Aerodynamik, Bd. II, 2. Aufl.

kulationsverteilung y(rj) in der Form:

= /(ч)г(ч) + 27/I/ (7-68)

-1

In abgekiirzter Form kann man die Integralgleichung der einfachen Traglinientheorie folgendermaBen schreiben:

= <*.(>?) + /МуМ – (7-69)

Die dimensionslose Zirkulationsverteilung 7(77) hangt mit der Auf – triebsverteilung dAjdy und dem ortlichen Auftriebsbeiwert

ca(y) = dAlqx l(y) dy

unter Beachtung von Gl. (7.5) zusammen durch:

Eine wichtige Eigenschaft von Gl. (7.68) besteht darin, daB fur ver- schiedene vorgegebene Anstellwinkelverteilungen oc^rj) und oc2(rj) die zugehorigen Zirkulationsverteilungen y1{rj) und y2(v) linear iiber – lagert werden konnen:

+ <*2(*7)>

y(v) =7iWl + УіМ-

Den Beiwert fur den Gesamtauftrieb erhalt man nach Gl. (7.59) zu:

1

CA = ^=Afy(y)dy. (7.72)

-1

Der Auftriebsanstieg wird hieraus erhalten, indem man die Zirkulations­verteilung des unverwundenen Fliigels yu fur <x = 1 berechnet. Somit ist

1

^ = yu(y)dr). (7.72a)

-1

Unter dem Nullauftriebswinkel oT0 eines symmetrisch verwundenen Fliigels verstehen wir nach Кар. 5.32 denjenigen Anstellwinkel, bei dem der Gesamtauftrieb Null ist. Man kann ihn in folgender Weise ermitteln: Zu der vorgegebenen Anstellwinkelverteilung ocv(r]), die gegen eine fliigelfeste Bezugsebene gemessen wird, errechnet man eine

Zirkulationsverteilung yv(rj) und nach Gl. (7.72) einen Gesamtauftriebs – beiwert cAv. Aus diesem erhalt man dann

^0 =-^cAv. (7.72b)

dcA

Es ist zweckmaBig, die Zirkulationsverteilung des verwundenen Fliigels bei einem beliebigen Anstellwinkel darzustellen durch lineare Super­position der Verteilung des unverwundenen Fliigels yu und einer Null – verteilung y0 des verwundenen Fliigels, fiir welche

і

cao = Л J y0(v)dr] = 0,

d. h. der Gesamtauftrieb gleich Null ist. Somit gilt fiir die Zirkulations­verteilung des verwundenen Fliigels bei beliebigem Anstellwinkel <x:

У (у) = <*Уи(ч) + Уо(у)- (7-73)

Die Nullverteilung y0(rj) beschafft man sich folgendermaBen:

Уо(у) = Vv(y) + *~оУи(г})-

Ahnlich wie fiir den Auftriebsbeiwert findet man fiir den Beiwert des Rollmomentes um die x-Achse (Vorzeichen nach Abb. 7.59):

і

Cl = = ~Л j l7-74)

-1

/ v(v)*)dr)

Haufig interessiert auch noch der seitliche Abstand des Auftriebsschwer – punktes einer Flilgelhalfte. Dieser wird:

Der Beiwert des induzierten Widerstandes ergibt sich nach Gl. (7.6) zu:

і

Си, і = yL = л /7 (r/) Лі (T>) dr] ■ (7-76)

-і

7.332 Losung durch Fourier-Polynome. Eine bequeme Methode, die Gl. (7.68) fiir die Zirkulationsverteilung zu losen, besteht darin, fiir die

Zirkulationsverteilung ein Fourier-Polynom

M

y(0) = 2 2>nsinn# (7.77)

n= 1

anzusetzen, wobei

cos & = « = (0 ^ & £ n) (7.78)

die dimensionslose Spannweitenkoordinate ist. Dieser Ansatz wurde von E. Trefftz [72] und H. Glauert [18] erstmalig eingefiihrt. Das erste Glied in Gl. (7.77) stellt die elliptische Zirkulationsverteilung у = 2a1sin# = 2ax Уі — rj2 dar, die bereits in Кар. 7.14 behandelt wurde. Setzt man die Gin. (7.77) und (7.78) in (7.67) ein, so erhalt man fur den induzierten Anstellwinkel

/ q X”[6] sill 71’O’ / —

«І (#) = 2 na« ~—г • 7- ‘9

n=l sin#

Dabei ist nach [18], vgl. Gl. (6.73),

71

1 Г cos nO’ d$’ — s*n n^

71 J COS O’ — COS O’ sin O’

0

Fuhrt man die Gin. (7.77) und (7.79) in (7.69) ein, so ergibt sich die folgende Bestimmungsgleichung fur die Fourierschen Koeffizienten an:

M

oc(0) sin 0 = ^ an[2/(#) sin# + n sin nO. (7.80)

71= 1

Hierbei sind die Verteilungen des Anstellwinkels <x(0) und des Fliigel – grundrisses f(0) gegeben. Die Koeffizienten av a2, . . ., aM werden dadurch bestimmt, daB man Gl. (7.80) in M Aufpunkten 0V #2, . . ., 0M langs der Spannweite erfiillt. Hierbei ergibt sich ein lineares Gleichungs – system fur ax bis ам. I. Lotz [51] hat die Durchfuhrung dieser Rech – nung dadurch noch vereinfacht, daB fur die Funktionen oc(0) sin# und f(0) sin# ebenfalls Fourier-Polynome eingefiihrt werden. Nachdem die Fourier-Koeffizienten an bestimmt worden sind, erhalt man aus Gl. (7.77) die Zirkulationsverteilung und aus Gl. (7.70) die Verteilung der ortlichen Auftriebsbeiwerte.

Den Beiwert fur den Gesamtauftrieb findet man nach Gl. (7.72) durch Einfiihrung der Gin. (7.77) und (7.78) zu

Fur den Beiwert des Rollmomentes wird entspreehend aus Gl. (7.74):

cL=-jAa2. (7.82)

Der Beiwert des induzierten Widerstandes ergibt sich aus Gl. (7.76) nach Ausfiihrung der Integration zu

M

cWi = % A 21 паї,* (7.83)

n—1

Fiihrt man hier cA nach Gl. (7.81) ein, dann kann man auch schreiben:

r2 M

cWi = ^-+nAZnal (7.83a)

nA n=2

Hierin stellt das erste Glied den Wert fiir die elliptische Zirkulations – verteilung dar, vgl. Gl. (7.24). Da der zweite Term in Gl. (7.83a) immer positiv ist, folgt sofort der wichtige Satz, dafi der induzierte Wider – standsbeiwert fur die elliptische Zirkulationsverteilung ein Minimum ist. Dieses gilt fur festgehaltenes Seitenverhaltnis Л und festgehaltenen Auftriebsbeiwert cA. Diesen Satz hat zuerst M. Munk [59] bewiesen.

7.333 Tragfliigel mit elliptischem Grundrifi. In Кар. 7.14 wurde der elliptische Tragfliigel bereits behandelt. Dort wurde gezeigt, daB ein unverwundener elliptischer Fliigel elliptische Zirkulationsverteilung iiber Spannweite besitzt. Der elliptische Fliigel mit Verwindung laBt sich nach den vorstehenden Formeln sehr einfach berechnen, wie u. a. H. Schmidt

[68] gezeigt hat.

Fiir den elliptischen Fliigel ist l = l( |/1 — ry2 = sin?? und A = und somit nach Gl. (7.65 c):

2sin #/(#) = ^ = fc.

OO

Fiir c’Aoq = 2 л ist die Konstante к = Л/2.

Setzt man Gl. (7.84) in (7.80) ein, dann wird

M

0C(&) sin?? = 21 (^ + n) «rjSinn??.

n=1

Hieraus lassen sich die Koeffizienten an durch eine Fourier-Analyse sofort berechnen zu 1

<*(#) = rm

Es moge diese Losung fur einige besonders einfache Anstellwinkel – verteilungen noch diskutiert werden. Setzt man

dann ergibt sich mit an = 0 fur n =f= m und mit am = rm/(fc + m) fur n = m die zugehorige Zirkulationsverteilung zu

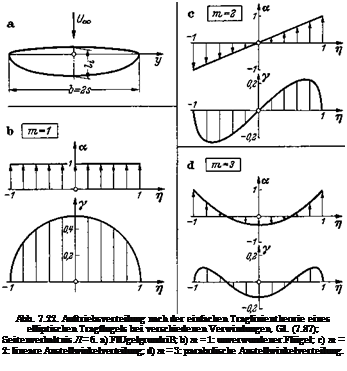Fiir einen Fliigel mit dem Seitenverhaltnis Л = 6, d. i. к == 3, sind die Ergebnisse fiir m = 1, 2 und 3 in Abb. 7.22 dargestellt. Esbedeutet

ш = 1 die konstante Anstellwinkelverteilung (unverwundener Fliigel), m = 2 die lineare Anstellwinkelverteilung, wie sie z. B. bei einer Roll – bewegung auftritt, und m = 3 die parabolische Anstellwinkelverteilung (symmetrische Verwindung, cA = 0).

Die Zirkulationsverteilung so wie die Beiwerte fiir den Auftrieb, das Rollmoment und den induzierten Widerstand des elliptischen ver-
wundenen Fliigels erhalt man nach den Gin. (7.77) und (7.81) bis (7.83), wenn man die entsprechenden Koeffizienten an nach Gl. (7.86) einsetzt. Dabei ergibt sich fiir den Auftriebsbeiwert

n

cA = -^4- — f <x(#) sin2# d&. (7.89)

* + 1 я J

0

Fiir den unverwundenen Fliigel, oc — const, folgt hieraus fiir den Auf – triebsanstieg in tJbereinstimmung mit Gl. (7.29):

d _____ TlA. _____ Сд op

doc к – f – 1 ^ Cji oo

+ ~лЛ

Aus den Gin. (7.89) und (7.89a) ergibt sich fiir den Nullauftriebswinkel:

+i

(7.89b)

-і

Fiir iiberschlagige Rechnungen lassen sich die fiir den Ellipsenfliigel angegebenen Beziehungen auch fiir andere Fliigelformen verwenden.

7.334 Quadraturverfahren yon Multhopp. Das einfachste und am meisten angewendete Verfahren zur Berechnung der Auftriebsverteilung von ungepfeilten Tragfliigeln nach der einfachen Traglinientheorie stammt von H. Multhopp [56].

Wir iibernehmen den Fourier-Ansatz nach Gl. (7.77) fiir die Zirku- lationsverteilung in der Form

M

У (#) = 2 £ % sin/*#. (7.90)

/M=l

Die Koeffizienten dp erhalt man durch eine Fourier-Analyse zu 1 r M.

y(#) sinju&d& = —- 2J Уп sm(7.91)

71 J и + n=1

о

wobei das Integral durch eine Summenformel ausgewertet wird.1 Hierbei ist

К = und Vn = COS . (7.92)

Ferner bedeuten yn = y(&n) = y(Vn) die Zirkulationswerte an den Stellen rjn.

Fiihrt man den Summenausdruck fiir a^ aus Gl. (7.91) in Gl. (7.79) ein, dann erhalt man fiir den induzierten Anstellwinkel

Da die innere Summe nur trigonometrische Funktionen enthalt, kann sie universell tabuliert werden. Dabei werden nach H. Multhopp fiir # aquidistante Werte

V7Z

M+ 1

gewahlt. Dieses bedeutet, daB der induzierte Abwindwinkel an den diskreten Stellen rj9 = cos#v berechnet wird. Bezeichnet man oci(rjv) mit <xiv, so laBt sich Gl. (7.93) in der einfachen Form schreiben :[7]

M

b„yv — 27 brny„ (v = 1, 2M).

n— 1

, _ * и sin[8]/ Uyv

sin jbl&v sin jbl&n M +1 sin #„ 1 — (— 1)^ sin #w 2(M + 1) (eos#„ — cos#n)2

Hierin ist:

Fiihrt man den Ausdruck Gl. (7.95) fiir den induzierten Anstellwinkel in die Bestimmungsgleichung fiir die Zirkulationsverteilung Gl. (7.69) ein, so erhalt man das folgende lineare Gleichungssystem fiir die Werte yv:

M

by у„ = <%, + 2′ Ъ,

n~ 1

Dabei ist die Abkiirzung

о h

by = bVy + fv=b„ + – p – (7.98)

Ceoo^v

eingefiihrt worden. Gl. (7.97) ist ein System von M linearen Gleichungen fur die M Zirkulationswerte y9 = y(r}v) mit v — 1, 2, . . ., M. In den Gin. (7.97) und (7.98) bedeuten ferner

ocv = oc(r]v) und lf = l(Vv).

Die fur M = 7 und M = 15 nach Gl. (7.96) universell berechneten Koeffizienten sind in Tab. 7.1 und 7.2 zusammengestellt. Die Werte bvn fiir v — n = 2, 4, . . . sind gleich Null.

Tabelle 7.1. Universelle Koeffizienten bvv und bvn fur die Berechnung der Zirlcu – lationsverteilung nach Mtjlthopp [56], fur M = 7, nach 01. (7.96). V і (7) 3 (5) 2 (6) 4 Vv 0,9239 0,3827 0,7071 0,0000 Кг 5,2262 2,1648 2,8284 2,0000 n n 2(6) 1,8810 0,8398 1(7) 1,0180 0,0560 4(4) 0,1464 0,8536 3(5) 1,0972 0,7887 Vvn 6(2) 0,0332 0,0744 5(3) 0,0973 0,7887 — — — 7(1) 0,0180 0,0560 І. 2 1,9142 0,9142 1 1,0360 0,1121 t>vn 4 0,1464 0,8536 3 1,1944 1,5774 h " 2 1,8477 0,7654 1 1,0000 _ ovn — — — 3 1,0000 —

Fur die numerische Losung des Gleichungssystems ist es bedeutungs – voll, daB das System der M Gleichungen in zwei Systeme von (M + l)/2 bzw. (M — l)f2 Gleichungen aufgespalten werden kann, die in bequemer Weise iterativ gelost werden konnen.

Fur M — 7 lauten die beiden Gleichungssysteme folgendermaBen:

biYi = *1 + ьізУз + bii7i + &івУв ЪзУз = «з + ЬзгУг + ЬзіУі + &зеУв ЪъУь = «5 + ЬьгУг + ььіУі + Ьь «Ге Ь7у7 = «7 + &72 Уз + Ь7 іУ і + &7вУб

ь2у2 = <х2 + Ь2іУі + Ь23у3 + Ь25у5 + Ь27у7 Ьіуі — «4 -|- ЬііУх – і’ bi3y3 – f Ьі6у5 + bi7y7 ьвУв — лв Н" ЬвіУі ьвзУз ЬзъУъ ЬбчУт

Tabelle 7.2 Universelle Koeffizienten bvv und bm fiir die Berechmtng der Zirkulationsverteilumg nach Multhopp [56], fur M = 15, nach 01. (7.96).

Das Gleichungssystem Gl. (7.97) und damit Gl. (7.99) gilt fur einen ungepfeilten, aber sonst beliebigen Fliigel von einigermaBen groBem Seitenverhaltnis (Л > 3) sowie auch fur eine beliebige Anstellwinkel – verteilung.

Es mogen jetzt noch die Vereinfachungen angegeben werden, die sich fur einen symmetrischen FlugelgrundriB und fur eine symme – trische bzw. antimetrische Anstellwinkelverteilung ergeben.

Symmetrische Anstellwinkelverteilung. Fur die zugehorige Zirkulationsvertei – lung gilt yn = У(м+і)—п• Setzt man dieses in Gl. (7.97) ein, dann wird

M+1 2

bvyv = (Xv + Z’ ЬтУп

n=1

mit

Die Koeffizienten byn sind fur M = 7 in Tab. 7.1 und fur M = 15 in Tab. 7.2 mit angegeben.

Antimetrische Anstellwinkelverteilung. Fiir die zugehorige Zirkulationsverteilung gilt yn — —ущ+1)_71. Setzt man dieses in Gl. (7.97) ein, dann wird

M-1

2

bvyv — (Xv + JJ’ bvn Уп (v = 1, 2, …,——————– (7.101)

n=i 2 /

mit

bvn = bvn — bvn (^ ~ M “Ь 1 — n). (7.101a)

Auch die Koeffizienten bm sind in den Tab. 7.1 und 7.2 angegeben.[9]

Die Konvergenz und die Genauigkeit dieses Rechenverfahrens wurde von H. Multhopp [56] eingehend untersucht. Das Verfahren konvergiert um so besser, je groBer das Seitenverhaltnis ist. Fiir stetigen Verlauf der Fliigeltiefe l(rj) und des Anstellwinkels (x(rj) reichen im allgemeinen M = 15 Punkte langs der Spann – weite fiir praktische Zwecke aus. Bei unstetigen Anstellwinkelverteilungen, wie sie bei Klappenausschlagen vorliegen, empfiehlt H. Multhopp eine Abspaltung der Unstetigkeitsstellen, bevor das oben angegebene Rechenverfahren angewendet wird, s. Кар. XII.

Den Beiwert des Oesamtauftriebes erhalt man nach Gl. (7.81). Hier – fiir laBt sich mit Gl. (7.91) schreiben:

Der Gesamtauftrieb ergibt sieh allein aus der symmetrisehen Zirku- lationsverteilung, mithin ist

M+1

Сл = Л2А, у,. (7.102)

V — 1

Dabei sind die Koeffizienten Av fur M = 1 und M = 15 in Tab. 7.3 angegeben.

Fur den Beiwert des induzierten Widerstandes erhalt man durch Anwenden von Gl. (7.91a) auf Gl. (7.76) die folgende Formel:

Die (xin werden dabei nach Gl. (7.95) berechnet.

Der Beiwert des Rollmomentes ergibt sich nach Gl. (7.82) und Gl. (7.91)

Zum Rollmoment liefert nur die antimetrische Zirkulationsverteilung einen Beitrag, mithin ist

M-1 2

CL — Л 2 Dvyv.

V=1

Auch die Koeffizienten Dv sind in Tab. 7.3 wiedergegeben.

Den seitlichen Abstand des Auftriebsschwerpunktes einer Fliigelhalfte nach Gl. (7.75) kann man bei symmetrischer Auftriebsverteilung wie folgt berechnen:

(7.105)

(7.106)

Auch die Koeffizienten Bv und Cv sind in Tab. 7.3 enthalten.

Beispiele: Nachstehend mogen die Ergebnisse einiger Beispielrech- nungen mitgeteilt werden.

Zunachst sollen fiir einen unverwundenen Rechteckfliigel vom Seitenverhaltnis A — 6 fiir ос = 1 die Zirkulationsverteilung у (rf) langs der Spannweite und daraus die Beiwerte fiir Auftrieb und induzierten Widerstand des Fliigels berechnet werden. Die Ermittlung der Zirkulationsverteilung wird wegen der symmetrischen Anstell – winkelverteilung mit Hilfe des Gleichungssystems (7.100) unter Verwendung der Koeffizienten bvn aus Tab. 7.1 durchgefiihrt. Fiir M = 7 Aufpunkte ergibt sich mit den entsprechenden Fliigeldaten das folgende Gleichungssystem von vier Glei – chungen mit den vier Unbekannten yx bis y4:

7,1361 = 1 + l,9142y2 + 0,1464y4

4,0747y3 – 1 + 0,9142y2 + 0,8536y4 4,7383y2 = 1 + l,0360y4 + 1,1944y3 3,9099 y4 = 1 + 0,1121 y4 + l,5774y3.

Dabei wurde fiir den Auftriebsanstieg des Fliigelprofils c’a00 = 2л angenommen, d. h. es ist / = 6/jt = 1,91. Die Auflosung dieses Gleichungssystems ergibt die Zirkulationswerte у in der zweiten Spalte von Tab. 7.4.

Soil die Zirkulationsverteilung fiir M — 15 Aufpunkte berechnet werden, so wird das Gleichungssystem (7.100) mit den entsprechenden Werten bvn aus der Tab. 7.2 gebildet. Als Anfangswerte des Iterationsverfahrens konnen dabei die fiir M = 7 gefundenen Werte dienen. Man findet so die in Spalte drei von Tab. 7.4 angegebenen Werte von y. Mit diesen Werten ergibt sich der Auftriebsanstieg nach Gl. (7.102) zu dcjdoc = 4,53. Fiir den induzierten Widerstand erhalt man aus Gl. (7.103) mit Gl. (7.95) beim Anstellwinkel a = 1 den Wert cwi — 1,14. Damit ergibt sich fiir den Fliigel mit konstanter Fliigeltiefe cwi = 1,05 с^/лЛ, d. h. ein um 5% groBerer induzierter Widerstand als fiir den elliptischen Tragfliigel mit gleichem Seitenverhaltnis.

Um den EinfluB des Seitenverhaltnisses auf die Auftriebsverteilung zu zeigen, wurden fiir drei unverwundene Rechteckfliigel vom Seiten­verhaltnis Л = 6, 9 und 12 die Zirkulationsverteilungen fiber Spann­weite berechnet. Mit wachsendem Л nahert sich die Zirkulationsvertei-

Tabelle 7.4. Zirkulationsverteilung tines Rechteckfliigels Л — 6 nach dem Berech – nungsverfahren von H. Mtjlthopp [56] fur M = 7 und M = 15 Aufpunkte. V У M = 7 M = 15 0 0,4320 0,4319 0,1951 — 0,4289 0,3827 0,4192 0,4193 0,5556 — 0,4012 0,7071 0,3710 0,3711 0,8315 — 0,3232 0,9239 0,2485 0,2497 0,9808 — 0,1446 1 0 0

lung mehr und mehr der rechteckigen Verteilung. Dieses erkennt man aus Abb. 7.23, in welcher die auf den Gesamtauftriebsbeiwert cA be – zogenen ortlichen Auftriebsbeiwerte ca йЬег der Spannweite aufgetragen

Abb. 7.23. Auftriebsverteilung CuIca von unverwundenen Rechteckflugeln vom Seitenverhaltnis Л = 6, 9,12 sowie Grenzkurven ftir Л -> 0 und Л —> oo (c’ = 2 n). A OO

sind. Fur Л -> oo (ebenes Problem) ist cJcA = 1, und fur sehr kleines Seitenverhaltnis (Л 0) ist die Auftriebsverteilung elliptisch.[10] Es moge hier angemerkt werden, daB die Auftriebsverteilung von un­verwundenen Rechteckfliigeln von A. Betz [1] nach einem anderen

Verfahren schon sehr frtih ermittelt wurde. Die Auftriebsanstiege fiir die Rechteckfliigel werden spater in Abb. 7.30 angegeben.

Um den EinfluB der Fliigelzuspitzung auf die Auftriebsverteilung zu zeigen, sind in Abb. 7.24 die Zirkulationsverteilungen fiir vier un – verwundene Trapezflugel vom Seitenverhaltnis A = 6 und mit den Zuspitzungen X = IJli — 0,1/4, x/2 und 1 dargestellt. Die Zuspitzung hat einen starken EinfluB auf die Verteilung des ortlichen Auftriebs-

beiwertes langs Spannweite. Dieses erkennt man aus Abb. 7.25, in welcher die Kurven calcA aufgetragen sind. Die stark zugespitzten Fliigel haben in der Nahe der Fliigelenden ortliche Auftriebsbeiwerte ca, die erheblich groBer sind als der Gesamtauftriebsbeiwert cA. Diese Tatsache ist bedeutungsvoll fiir das AbreiBverhalten der Stromung solcher Fliigel – formen bei hohen Auftriebsbeiwerten. Bei Steigerung des Anstellwinkels tritt der Ablosungsbeginn etwa an der Stelle des maximalen ortlichen Auftriebsbeiwertes auf, somit bei stark zugespitzten Trapezfliigeln in der Nahe der Fliigelenden und bei Rechteckfliigeln in der Fliigel – mitte.

7.335 Ringflugel. Auf die Behandlung von Tragfliigelsystemen, wie z. B. Doppeldecker – und Tandemanordnung, wollen wir verzichten, da diese fiir die Flugtechnik keine groBe praktische Bedeutung mehr haben. Jedoch soli hier noch eine Sonderform, namlich der Ringfliigel, kurz erwahnt werden.

Abb. 7.26. Auftriebsanstieg eines Ringflugels in Abh&ngigkeit vom Seitenverhaltnis. Kurve 1: einfache Traglinientheorie nach Gl. (7.108); Kurve 2: Tragfiachentheorie nach [81]; Messungen vgl. [16].

Unter einem Ringfliigel verstehen wir eine rohrenformige zylin – drische Flache nach Abb. 7.26. Mit D als Durchmesser und L als Tiefe definiert man

als das Seitenverhaltnis des Ringfliigels. Bei unsymmetrischer An – stromung unter dem Anstellwinkel oc erfahrt ein solcher Ringfliigel einen Auftrieb, der sich nach ahnlichen Verfahren berechnen laBt wie der Auftrieb des gewohnlichen Tragfliigels. Im einfachsten Fall (Trag­linientheorie) wird der Ringflugel durch eine kreisformige tragende

Linie ersetzt. Mit der Theorie des Ringflugels hat sich besonders ein – gehend J. Weissinger [84] befaBt.

Bezieht man den Auftriebsbeiwert auf die abgewickelte Zylinder- flache, also

A = cAnDLq

so gilt nach der einfachen Traglinientheorie fur den Auftriebsanstieg:

dcA __ 2пЛ

doc n + 2Л

In Abb. 7.26 ist der Auftriebsanstieg in Abhangigkeit vom Seiten- verhaltnis Л dargestellt. Zum Vergleich sind Messungen verschiedener Autoren eingetragen, die befriedigend mit dieser einfachen Theorie ubereinstimmen. Eine bessere Gbereinstimmung der Messungen mit der Theorie ergibt sich, wenn man Ergebnisse nach der erweiterten Traglinientheorie und nach der Tragflachentheorie zum Vergleich heranzieht. Es sei hierzu wieder auf die Arbeit von J. Weissinger [84] verwiesen.