Elemental Error Sources

The elemental error sources of TSP have been discussed by Cattafesta et al. (1998) and Liu et al. (1995c). Table 7.2 lists the elemental error sources, sensitivity coefficients, and total uncertainty of TSP. The sensitivity coefficients for many variables are related to (p=KT/(T _Tre/). The elemental errors in the

variables Dt(At) , Dx(Ax ) , Dq0(At) , V, Vre/ , Пстсге/ , П//П/re/ , h/hre/r

c/cre/, and q0/q0re/ can be estimated using the same expressions given in the

uncertainty analysis for PSP, which represent the error sources associated with model deformation, unstable illumination, photodegradation, filter leakage, and luminescence measurements. The camera calibration error and temperature mapping error can be also estimated using the similar expressions to those for

PSP, i. e., var(T) ~(dT/dx) a22 +(dT/9y)a2 and var(T) = |(VT)surf • (AX)/ ,

where ax and ay are the standard deviations of least-squares estimation in image

registration or camera calibration. In order to estimate the TSP calibration errors, the temperature dependency of TSP was repeatedly measured using a calibration set-up over days for several TSP formulations (Liu et al. 1995c). Temperature measured by TSP was compared to accurate temperature values measured by a
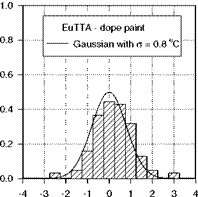
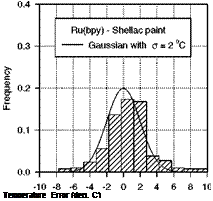
standard thermometer. Figure 7.22 shows histograms of the temperature calibration error for EuTTA-dope and Ru(bpy)-Shellac TSPs, which exhibit a near-Gaussian distribution. The standard deviation for EuTTA-dope TSP is about 0.8oC over a temperature range of 15-70oC. For Ru(bpy)-Shellac TSP, the histogram has a broader error distribution having the deviation of about 2oC over a temperature range of 20-100oC.

The temperature hysteresis introduces an additional error source for TSP, which was reported in calibration experiments for a Rhodamine(B)-based coating (Romano et al. 1989). The temperature hysteresis is related to the polymer structural transformation from a hard and relatively brittle state to a soft and rubbery one when temperature exceeds the glass temperature of a polymer. Since the thermal quenching of luminescence in a brittle condition is different from that in a rubbery state, the temperature dependency is changed after it is heated beyond the glass temperature. To reduce the temperature hysteresis, TSP should be pre­heated to a certain temperature above the glass temperature before it is used as an optical temperature sensor for quantitative measurements. It was found that for both pre-heated EuTTA-dope and Ru(bpy)-Shellac paints the temperature hysteresis was minimized such that the temperature dependency remained almost unchanged in repeated tests over several days (Liu et al. 1995c).

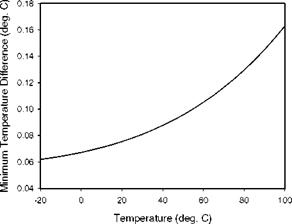
Fig. 7.21. The minimum resolvable temperature difference as a function of temperature for a Ruthenium-based TSP for (nperef )max = 500,000e, KT = 37.7oC, and Tref = 20oC

(b)

Fig. 7.22. Temperature calibration error distributions for (a) EuTTA-dope TSP and (b) Ru(bpy)-Shellac TSP, where о is the standard deviation. From Liu et al. (1997b)

Table 7.2. Sensitivity coefficients, elemental errors, and total uncertainty of TSP Variable Sensi. Elemental Variance Physical Origin Z Coef. Si var( Ci) 1 Dt(At) <p [(dV/dt)( At)/V][2] [3] [4] Temporal variation in luminescence due to photodegradation and surface contamination 2 DJAx ) V [ (dV/dx)2 a2 +(3V/3y)2 a 2y ]V-2 Image registration errors for correcting luminescence variation due to model motion 3 Dqo(At) V [( dq0/ d t)( At)/q0ref]2 Temporal variation in illumination 4 Vrf V Vref G Й V Bd Photodetector noise 5 V -(p VG hv Bd Photodetector noise 6 n cm Cref <p [R2/(Rj + R2 )]2(ARi/Ri )2 Change in camera performance parameters due to model motion 7 П //П f ref V var(nf/Пfref ) Illumination spectral variability and filter spectral leakage 8 h/href (p [(dh/дx)2a2 + (h/дy)2a2 ]h-f Image registration errors for correcting thickness variation due to model motion 9 C/Cref V [ (dc/d x) al + (Эс/Э y) a 2 ] c-^ Image registration errors for correcting concentration variation due to model motion 10 q0/q0ref V (%г4Ґ( Vq0) • ( AX ) Illumination variation on model surface due to model motion 11 KT 1 var( KT) Paint calibration error 12 Temperature mapping 1 (dT/dx)2 a2 + (dT/dy) a2y Errors in camera calibration and temperature mapping on a surface of and ( VT)sllf • ( AX )f a presumed rigid body

M

Total Uncertainty in Temperature var(T)/(T – Tref )2 = ^ Si2 var( )/Ct2

i = 1