Ground Effect

When a finite wing (and airplane) operates near the ground within a distance of approximately 20 percent of the wing span, as in landing or takeoff, the wing behavior is modified from that observed in an unrestricted freestream. This is called ground effect, and it may be explained by referring to the wing-lifting-line model.

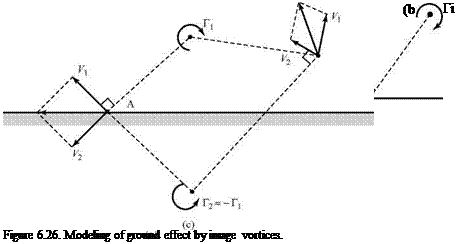
Let a lifting wing be represented by a horseshoe vortex, as shown in Fig. 6.26a. For simplicity, we consider a vertical plane that encloses one trailing-tip vortex and let the plane be sufficiently far downstream so that the flow in the plane may be assumed as two-dimensional. If a solid surface is inserted below the trailing vortex as in Fig. 6.26b, the boundary condition to be satisfied is that the flow must be tangent to that surface. However, the trailing vortex induces a vertical-velocity component at the surface and the boundary condition is not satisfied. This means that the flow physically must adjust to be tangent to the surface; however, a single vortex is too simple a model to satisfy this requirement. This problem must be resolved by intro­ducing an image vortex at the same distance below the surface as the trailing vortex
is above. The image vortex has the same strength as the trailing vortex but the oppo­site sense, as shown in Fig. 6.26c.

At any Point A on the surface, the superposing of the induced velocity V1 due to the trailing vortex Г j with the velocity V2 due to the image vortex results in a cancel­lation of the vertical-velocity component at the surface, and the tangency-boundary condition thereby is satisfied. Notice, however, that the velocity at any Point B within the flow field is modified by the presence of the image vortex so that the velocity at Point B is not identical to what it would be in an unconfined flow.

Now, visualize this picture extended into three dimensions, with the lifting wing close to a surface being represented by a lifting line and a trailing-vortex sheet. A mechanism still must be present to satisfy the tangency-boundary condition at the ground plane. The required image-vortex sheet modifies the unconfined flow; in particular, it significantly modifies the downwash at the lifting line.

The effect of the image-vortex sheet is that the downwash at the wing is consider­ably reduced and the wing lift-curve slope is increased. Because the downwash (and induced angle of attack) is decreased, the induced drag also is reduced. The net effect on the aircraft of the increase in lift (at the same angle of attack) and decrease in drag is that just before touchdown, the aircraft briefly seems to be buoyed up and floating. During the interaction, the aircraft is said to “flare,” or manifest ground effect. Some­times the flare maneuver is supplemented by an increase in the angle of attack that can exceed the stalling angle at altitude. This allows touchdown at the lowest possible speed so that landing loads are minimized and rollout thereby is shortened.

The concept of using image vortices to represent the effect of a solid wall may be used to correct for the effect of the solid wall in a wind-tunnel test section. When an overly large model is tested, the requirement that the flow be tangent to the solid wall induces significant changes in the flow field compared to that of flight in the atmosphere in which the flow is not so constrained. By representing the effect of the wind-tunnel walls with image vortices, the effect of the solid wall on the measured data can be estimated and the data corrected accordingly.