PREVENTION OF THE STALL FLUTTER
According to Eq. 1 of § 9.4, the critical stall-flutter speed can be raised by increasing the frequency of free torsional oscillation of the blade, i. e., by increasing the torsional stiffness and reducing the mass moment of inertia.
Stall flutter can be delayed if the airfoil can be prevented from stalling. Thus, in designing propellers, care must be exercised to choose the proper airfoil section, and, if possible, the working angle of attack should be limited to below the stalling angle.
It is shown by Theodorsen and Regier4,36 that the divergence speed of a propeller is an important parameter to consider in connection with the stall flutter (see § 4.8). If the rotational speed of a propeller is so high that the relative wind speed is close to the critical-divergence speed, the
blade will be twisted excessively, possibly beyond the stalling angle, and thus causing stall flutter. Theodorsen and Regier show that, for several models of wind-tunnel propellers tested in the high-angle-of-attack range (with initial settings below the stalling angle), flutter invariably occurs at a speed substantially below the classical flutter speed. The angle of attack of the blade at which flutter occurs appears to be nearly constant and independent of the initial blade setting. Apparently the blade simply
|
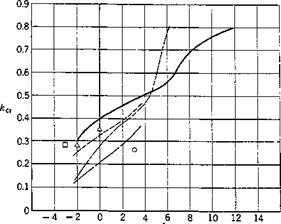
Да — а і mean ~ ** static stall ————– NPL, R = 1.42 x 105, в = 2.0°, Axis of rotation, mid-chord. ————– NPL, R = 1.42 x 10®, в = 6.0°, Axis of rotation, mid-chord. ————– NPL, R = 2.83 x 10°, в = 2.0°, Axis of rotation, mid-chord. ————– NPL, Д = 2.83х 1O5,0 = 6.0°, Axis of rotation, mid-chord. ”□Blunt wing Д = 0.84×10® MIT j a Intermediate 0 = 6.08° Sharp wing 0 = pitch amplitude Axis of rotation, 37% chord. Ref. NPL: ARCR&M 2048; MIT: NACA TN 2533 Fig. 9.11. Critical reduced frequency. |
twists to the stalling angle, and flutter starts. Furthermore, Theodorsen and Regier show that the classical flutter speed and the divergence speed of a propeller are approximately the same because of the centrifugal force effect. The problem of predicting propeller flutter is thus resolved primarily into the calculation of the speed at which the propeller will be twisted to stall. This can be done by methods of Chapter 3.
As to the practical design measures to raise the critical stall-flutter speed, we may quote an interesting case reported by Sterne and Brown.7-141
They tested on a spinning tower a variable-pitch propeller fitted with compressed wood blades. The airfoil sections of the blade inboard of the 75 per cent radius were of conventional Clark shape, but outboard of the 75 per cent radius they had an undercamber. Serious flutter was encountered when the blades were set at angles larger than 20° at the 70 per cent radius. But, when the blades were set at 19° and less, there was no evidence of flutter. The difference in the flutter characteristics at the blade-angle settings of 20° and 19° was very pronounced. It appeared that the flutter was stall flutter. A pitch setting of 20° corresponded to a lift coefficient CL of about 1.0 at the tip sections. The propeller was then modified by the removal of part of the leading edge of the sections outboard of 75 per cent radius, and reshaping the cross sections near the blade tips into the conventional Clark form. This modification had the effect of bringing the center of pressure further back, relative to the centroids of the inboard sections, so that the torsional deflection of the blades became smaller. The modified propeller was then retested. No flutter was encountered for blade settings up to 22° at the 70 per cent radius.
So far our attention is directed toward stall flutter at low speed of flow (incompressible fluid). The stall-flutter problem of high-speed aircraft is complicated not only by the effect of the compressibility of the air, but also by the geometrical factors often associated with high-speed wing designs: low aspect ratio, thin wing sections, sweep angle, large masses attached to the wings, etc. To determine the effects of these items on the stall-flutter characteristics of a wing is a challenging problem for future research.