Sobieczky’s Rheograph-Transformations

Sobieczky [17] used Busemann normalized hodograph plane, where ф and ф (potential and stream function) can be written as Beltrami equations:

where q (and K) are functions of the local Mach number. The above linear system for generalized potentials, is hyperbolic for M > 1 (q (M) > 0) and elliptic for M < 1

(q(M) < 0).

For transonic plane flow, the values of ф and ф for the subsonic and supersonic parts are connected along the transformed sonic line, the axis q = 0.

Let, ф, ф(q = 0, в) = ф*, ф* (в). For the elliptic region, ф* and ф* are used to complete the formulation of an elliptic boundary value problem, and for the hyperbolic domain, ф* and ф* are initial values which describe the solution of the above equations in a triangular region of dependence. It should be mentioned that Sobieczky’s formulation of transonic boundary value problem is different from the well known Tricomi problem, since there is no prescribed boundary in the hyper­bolic region.

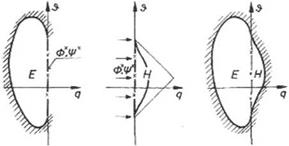
In the elliptic domain (q < 0), the elliptic system does not change its nature by conformal mappings. Sobieczky introduced several mappings called rheograph- transformations to facilitate the solution of the equations in the elliptic domain. He used electric analogy and conducting papers which have to be inhomogenized to vary the local conductivity to simulate the coefficient K in the governing equations.

On the other hand, the solution of the hyperbolic equations can be found by series expansion or by the method of characteristics, where the computation starts from the given sonic line.

In passing, for near sonic flows, where the mach number is close to one in the whole flow field, Sobieczky replaced q (M) and K (M) by the first term of their series expansions around M = 1. The governing equations take now the form of generalized axially symmetric potential equations treated by Weinstein, thus Sobieczky obtained

exact solutions in closed form which are identical to the solutions of the Tricomi equation.

The electric analogy together with the method of characteristics were used suc­cessfully to design supercritical wing sections as well as to design transonic cascades. For a given upstream velocity, the elliptic boundary value problem is defined and an analog model can be produced. Continuation of the analog model beyond the sonic line, using numerical methods, allows the calculation of the dependent supersonic flow region and hence the airfoil contour, see Fig. 13.6.

Later, Sobieczky introduced the method of fictitious gas, where the density is modified in the supersonic region, and the flow field is solved to produce the sonic line. The elliptic flow field with the sonic line are used to construct shock free airfoil via continuation based on the method of characteristics and the actual density in the supersonic region, to produce the contour of the airfoil adjacent to the supersonic flow. See Ref. [18] for more details (Notice that the direct extension to three dimensional flows over a wing leads to unstable calculations) (Fig. 13.6).