Sting-Mounted Model

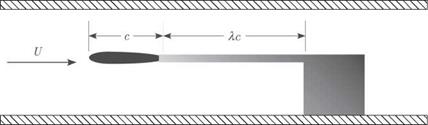
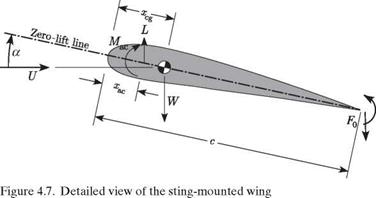
A second configuration of potential interest is a rigid model mounted on an elastic sting. A simplified version of this kind of model is shown in Figs. 4.5 through 4.7, in which the sting is modeled as a uniform, elastic, clamped-free beam with bending

1 в

stiffness EI and length Xc, where X is a dimensionless parameter. The model is mounted in such a way as to have angle of attack of ar when the beam is undeformed. Thus, as before, a = ar + в, where в is the nose-up rotation of the wing resulting from bending of the sting, as shown in Fig. 4.6. Also in Fig. 4.6, we denote the tip deflection of the beam as 5, although we do not need it for this analysis. Note the equal and opposite directions on the force F0 and moment M0 at the trailing edge of the wing in Fig. 4.7 versus at the tip of the sting in Fig. 4.6.

Figure 4.5. Schematic of a sting-mounted wind-tunnel model

From superposition, we can deduce the total bending slope at the tip of the sting as the sum of contributions from the tip force F0 and tip moment M0, denoted by в F and вм, respectively, so that

в = eF + вм

From elementary beam theory, these constituent parts can be written as

Two static aeroelastic equilibrium equations now can be written for the deter­mination of eF and вм. Using Eqs. (4.3) and (4.4) for the lift and pitching moment,

k\\\\\\\\\\\\\\\\\\\\\\\N Figure 4.8. Schematic of strut-supported wind-tunnel model

the force equilibrium equation can be written as

qSC!^ (a + вР + вы) – W — F0 = 0 (4.15)

and the sum of moments about the trailing edge yields

qScCMac + qSCLa (ar + eF + вМ) (c — xac) — W (c — xcg) — M0 = 0 (4.16)

Substitution of Eqs. (4.14) into Eqs. (4.15) and (4.16), simultaneous solution for eF and вМ, and use of Eq. (4.12) yields

2rac)

в

(4.17)

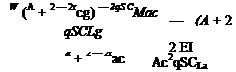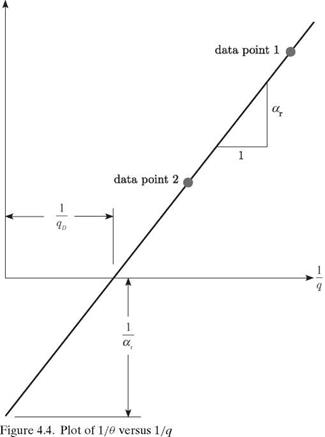
where rac = xac/c and rcg = xcg/c. Here again, the condition for divergence can be obtained by setting the denominator to zero, so that

qD c2 SA (A + 2 — 2rac) Cta (. )

However, unlike the previous example, we cannot make the divergence dynamic pressure infinite or negative (thereby making divergence mathematically impos­sible) by choice of configuration parameters because xac/c < 1. For a given wing configuration, we are left only with the possibility of increasing the sting’s bending stiffness or decreasing A to make the divergence dynamic pressure larger.