The Influence of the Mach Number and the Thermal State of the Surface
The original formulation of stability theory for compressible flow of L. Lees and C. C. Lin, [30], with the generalized point of inflection, led to the result that sufficient cooling can stabilize the boundary layer in the whole Reynolds and Mach number regime of flight [32].
This was an interesting finding, which could help to reduce the thermal load and drag problems of CAV’s, because such vehicles fly with cryogenic fuel. An appropriate layout of the airframe surface as heat exchanger would combine both cooling of the surface and stabilization of the attached laminar viscous flow past it. This would be possible even for flow portions with adverse stream-wise pressure gradient, because, as we can see from eq. (7.53), the influence of the pressure-gradient term can be compensated by sufficiently strong cooling. If then the flow past the flight vehicle would not become turbulent, the heating and drag increments due to the occurrence of transition, see Figs. 7.10 and 7.11, could be avoided.
Unfortunately this conclusion is not true. It was shown almost two decades later by L. M. Mack, [21], see also [18, 25], and the discussion in [13, 14], that for МГе1 > 1 higher modes (the so-called “Mack modes”) appear, which cannot be stabilized by cooling, in contrary, they are amplified by it. The first of these higher modes, the “second mode”—if the low-speed mode is called first mode—in general is of largest importance at high boundary-layer edge Mach numbers, because it is most amplified.[132] For an adiabatic, flat-plate boundary-layer higher modes appear at edge Mach numbers larger than Me « 2.2. At Me ^ 4 the second mode has a frequency low enough to definitely influence the instability behavior. This result is illustrated qualitatively in Fig. 8.4 for a boundary layer on an adiabatic flat plate.
At Me = 0, case a), only the classical (first) instability mode of incompressible flow exists. At Me = 4.5, case b), a second instability mode has appeared, which at Me = 5.8 has merged with the first mode.
If the wall is cooled, the second mode can become important already at low supersonic Mach numbers. The significant finding of Mack was that the second mode is amplified by cooling, whereas the first mode is damped by it.
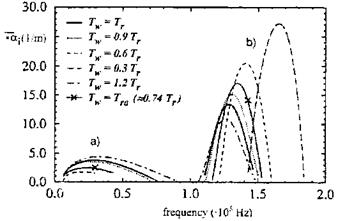
We show this effect with numerical results of E. Kufner in Fig. 8.5 [34], see also the experimental result of S. Willems and A. Gulhan in Section 10.6.
Kufner studied the dependence of the spatial amplification rates ai of the first and the second instability mode on the thermal state of the surface— the wall temperature Tw and implicitly the temperature gradient in the gas
|
Fig. 8.4. Temporal stability charts of the boundary layer at an adiabatic flat plate for different boundary-layer edge Mach numbers (cI = cQ. Qualitative presentation of the results of Mack, following Reshotko [13]: a) Me = 0, b) Me = 4.5, c) Me = 5.8. |
|
Fig. 8.5. Influence of the wall temperature Tw on the spatial amplification rates of a) the first, and b) the second instability mode in the boundary layer at a blunt 7° half-angle cone at M= 8, Re^ = 3.28-106 m-1, T^ = 54.35 K, a = 0°, location: S ~ 175 Rn ~ 667 mm [34]. Tr is the recovery, Tra the radiation-adiabatic wall temperature. |
normal to the cone’s surface dT/dngw. The case is the Ыж = 8 flow past a blunt cone (Stetson cone) with opening half-angle Фс = 7 ° and nose radius Rn = 3.81 mm. The location S is measured from the nose point along the generatrix of the cone surface.
The first instability mode, a), on the left-hand side of the figure (always the result for the wave angle with maximum amplification is given), exhibits the classical result, that with cooling, i. e., a wall temperature lower than the recovery temperature (Tw < Tr), the amplification rate is reduced and the maxima are shifted to smaller frequencies. This alone would lead to the
transition pattern indicated for increasing Mach number in Fig. 8.1, which is characterized by a widened and flattened transitional branch. In contrast to this, the second instability mode, b), on the right-hand side of the figure, is strongly amplified by cooling, with a shift of the maxima towards larger frequencies.[133]
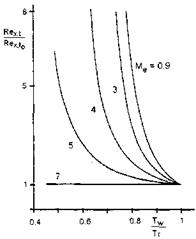
It was noted above that for sufficiently small external disturbance levels transition is governed directly by linear instability. Regarding the influence of the thermal state of the surface on the instability and transition behavior of the boundary layer, this appears to be corroborated by data of F. Vignau, Fig. 8.6, see [14].
|
Fig. 8.6. Results of a numerical study of the influence of wall cooling on the flat – plate transition Reynolds number at different boundary-layer edge Mach numbers Me. Rex, t is the transition Reynolds number at a given wall temperature, Rex, t0 that at the adiabatic wall, Tw the wall temperature, and Tr the adiabatic wall temperature. |
Results of the application of the en – method, a semi-empirical transition – prediction method, see Sub-Section 8.4.2, to flat-plate flow are in fairly good agreement with experimental trends. Fig. 8.6 shows the ratio of ‘transition Reynolds number at given wall temperature’ to ‘transition Reynolds number at the adiabatic wall’, Rex, t/Rex, t0, as function of the ratio ‘wall temperature’ to ‘adiabatic wall temperature’, Tw/Tr, for different boundary-layer edge Mach numbers Me.
The transition Reynolds number Rex, t for Me ^ 3 becomes progressively larger with smaller Tw/Tr. This is due to the reduction of the growth rate of the first instability mode, which is the only mode present at Me ^ 3. The boundary layer with surface cooling appears to be almost fully stabilized. For Me ^ 3 the transition Reynolds number Rex, t reacts less strongly on the decreasing wall temperature, because now the second instability mode exists which becomes amplified with wall cooling. For Me = 7 wall cooling has no more an effect. Although the use of a constant n = 9 in this study can be questioned, it illustrates well the influence of wall cooling on the transition behavior of a flat-plate boundary layer with hypersonic edge flow Mach numbers.