This also is compared with exact results in the figures that follow. SHORT-PERIOD MODE

Figure 9.26 shows that the speed remains substantially constant in the short-period mode, and this suggests an approximation to the equations in which = 0. Again, one equation must be dropped from the set, and the correct choice is the speed equation of motion. The reduced equations are

The characteristic equation is then

(CLa+CDe)

2ц

* Ifi Cm<SpLa + ! JL (/7 – L П ) _ s

r, r——————- ^—j iX ”*‘+

This expands to give the cubic equation

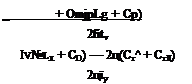S(s2 + Cxs + c0) = 0

of which the second-degree factor is the approximation for the short-period roots. The zero root is of no interest. With the numerical values of the preceding example, the roots obtained from (9.2,14) are

A = -.1162 x 10-1 ± .1892 x 10-1 і

which are to be compared to the exact values

-.1161 x 10-1 ± .1891 X 10-4

The errors are seen to he very small, less than to % in both the damping and the period. Equations (9.2,14) give a good approximation to the im­portant short-period oscillation over a wide range of flight and vehicle parameters.

Because of the large influence of C. G. position on Cm, a critical C. G. position is indicated by (9.2,14) when

+ Cmg(CLa + CDe) = 0 (9.2,15)

At this condition, c0 vanishes, and the characteristic equation becomes

«(* + сг) = 0

with roots X = 0, — cv The latter corresponds to a damped exponential mode, and the zero root identifies one that is a constant state in the two variables Да and q. This state, a longitudinal motion at constant speed, а and q is none other than the steady pull-up treated in Sec. 6.10. The critical C. G. position is found from (9.2,15) thus

Comparison of (9.2,16) and (6.10,8) shows that hceii above would be exactly hm (the control-fixed maneuver point) if CDe were zero in the former and CL^ zero in the latter. In fact these equations both describe the same flight condition, and the differences between them are entirely due to differences in the detailed assumptions made in their derivations. Specifically, CLq was neglected in (9.2,12) and no component of the thrust normal to V was included in the derivation of (6.10,8). Had the assumptions been strictly compatible, the results would have been identical.

The above analysis shows that the steady pull-up at constant speed can occur without motion of the controls at this C. G. position, and hence it is indeed the condition of zero control motion per g. We can further deduce that movement of the C. G. farther aft causes a reversal of sign of e0 and hence corresponds to a ‘‘static instability” as in a mass-spring-damper with a “negative” spring. In this light the control-fixed maneuver point is seen as a criterion for the divergence of the short-period mode.