Dirichlet Boundary Condition

In this case, the perturbation potential Ф has to be specified everywhere on SB. Equation (9.2a) does this exactly, and by distributing the singularity elements on the surface, and placing the point (x, y, z) inside the surface SB the inner potential Ф* in terms of the surface singularity distributions is obtained:

Again, these integrals are singular when r-*0 and near this point their principal value must be evaluated. The zero flow normal to the surface boundary condition (Eq. (9.4)) is defined now using Eq. (9.8). Therefore, the
condition У(Ф + Ф„) • n = 0, in terms of the velocity potential, becomes

Ф,* = (Ф + ФД = const.

or

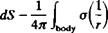dS + Ф* = const.

(9.10)

Equation (9.10) is the basis for methods utilizing the indirect boundary conditions. However, even at this stage, there are many differences between the various methods of solution, related to setting the value of the inner potential Ф* (in addition to the differences in the source/doublet combina­tions). For example, by setting Ф(* = (Ф + Ф„), = 0, Eq. (9.10) can be solved on the surface SB but the resulting singularity distribution will include Ф» and the strength will be large.

Other values for the inner potential can be specified too (not necessarily constant) and when the inner potential is set to Ф,* = (Ф + Ф„), = Ф* (which is equivalent to specifying Eq. (9.10) for the perturbation only in a “ground-fixed frame” where Ф„ = 0) then Eq. (9.10) reduces to a simpler form:

(9.11)

To justify the above, consider the Neumann boundary condition (Eq. (9.4)) ЭФ*/Эп = 0, which is equivalent to ЭФ/Эп = — n • Q„. Recall that the value for the discontinuity in the normal derivative of the velocity potential as given by Eq. (3.12) is

9Ф* ЭФ* ЭФ ЭФ,

° дп дп дп дп

and since Ф, = 0 then also ЭФ,/дп = 0 on SB. Consequently, for Eq. (9.11) to be valid, the source strength is required to be

<r = n-Qoo (912)

where n points into the body as in Fig. 9.1.

To define this problem uniquely, the wake doublet distribution should be known or related to the unknown doublets on SB (Kutta condition). To proceed with the solution, SB is divided into discrete elements and at each of these elements Eq. (9.10) (or Eq. (9.11)) is evaluated. This results in a set of algebraic equations for the unknown /x distribution. Note that when evaluating the integrals at a point P on the element (r—»0) then Ф(Р) = Т/х/2 (see Section 3.14).

In this formulation, when Eq. (9.12) is used, the zero normal flow boundary condition information is contained in the source terms and for very thin surfaces the integral may be ill-conditioned and will cause numerical instabilities.