Laminar and turbulent flows

Closer experimental study of boundary-layer flows discloses that, like flows in pipes, there are two different regimes which can exist: laminar flow and turbulent flow. In laminar flow, the layers of fluid slide smoothly over one another and there is little interchange of fluid mass between adjacent layers. The shearing tractions that develop due to the velocity gradients are thus due entirely to the viscosity of the fluid, i. e. the momentum exchanges between adjacent layers are on a molecular scale only.

In turbulent flow considerable seemingly random motion exists, in the form of velocity fluctuations both along the mean direction of flow and perpendicular to it. As a result of the latter there are appreciable transports of mass between adjacent layers. Owing to these fluctuations the velocity profile varies with time. However, a time-averaged, or mean, velocity profile can be defined. As there is a mean velocity gradient in the flow, there will be corresponding interchanges of streamwise momen­tum between the adjacent layers that will result in shearing stresses between them. These shearing stresses may well be of much greater magnitude than those that develop as the result of purely viscous action, and the velocity profile shape in a turbulent boundary layer is very largely controlled by these Reynolds stresses (see Section 7.9), as they are termed.

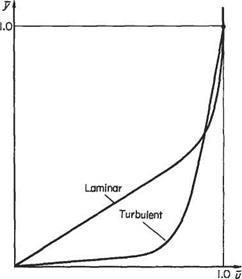
As a consequence of the essential differences between laminar and turbulent flow shearing stresses, the velocity profiles that exist in the two types of layer are also different. Figure 7.4 shows a typical laminar-layer profile and a typical turbulent – layer profile plotted to the same non-dimensional scale. These profiles are typical of those on a flat plate where there is no streamwise pressure gradient.

In the laminar boundary layer, energy from the mainstream is transmitted towards the slower-moving fluid near the surface through the medium of viscosity alone and only a relatively small penetration results. Consequently, an appreciable proportion of the boundary-layer flow has a considerably reduced velocity. Throughout the

Fig. 7.4 boundary layer, the shearing stress r is given by r = fi(du/dy) and the wall shearing stress is thus tw = fj(du/dy)y-0 = /i(<9u/<9y)w(say).

In the turbulent boundary layer, as has already been noted, large Reynolds stresses are set up owing to mass interchanges in a direction perpendicular to the surface, so that energy from the mainstream may easily penetrate to fluid layers quite close to the surface. This results in the turbulent boundary away from the immediate influ­ence of the wall having a velocity that is not much less than that of the mainstream. However, in layers that are very close to the surface (at this stage of the discussion considered smooth) the velocity fluctuations perpendicular to the wall are evidently damped out, so that in a very limited region immediately adjacent to the surface, the flow approximates to purely viscous flow.

In this viscous sublayer the shearing action becomes, once again, purely viscous and the velocity falls very sharply, and almost linearly, within it, to zero at the surface. Since, at the surface, the wall shearing stress now depends on viscosity only, i. e. rw = fi(du/dy)w, it will be clear that the surface friction stress under a turbulent layer will be far greater than that under a laminar layer of the same thickness, since (du/dy)w is much greater. It should be noted, however, that the viscous shear-stress relation is only employed in the viscous sublayer very close to the surface and not throughout the turbulent boundary layer.

It is clear, from the preceding discussion, that the viscous shearing stress at the surface, and thus the surface friction stress, depends only on the slope of the velocity profile at the surface, whatever the boundary-layer type, so that accurate estimation of the profile, in either case, will enable correct predictions of skin-friction drag to be made.