Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Multidimensional Waves
The analysis of the previous sections is primary for one-dimensional waves. However, it can easily be generalized to waves in two or three dimensions.
Suppose the multidimensional dispersion relation of a wave system is
 |
 |
 |
Again, assuming there is a simple pole on the real «-axis given by«(ai), it is straightforward to obtain by the Residue Theorem that the contribution of this pole to the solution is
 |
 |
 |
The triple integral may be evaluated asymptotically for large t by the method of stationary phase in multidimensions. Thus,
 |
 |
 |
where
 |
 |
 |
In Eq. (4.38), det is the determinant of and g depends on the number of factors of n/4 arising from path rotation. Now Eq. (4.39) gives the group velocity, Vi, in three dimensions as follows:
It is easy to see, for a multidimensional finite difference system, that the same analysis applies. Therefore, the conclusions concerning numerical dispersion and dissipation
obtained for a one-dimensional system are also true for multidimensional finite difference approximations.
EXERCISES 4.1. Suppose the initial value problem,
^ + c^r = 0, u(x, 0) = f (x),
dt dx
is computed by approximating the du/dx term by a finite difference quotient, show
(i) If the standard sixth-order central difference approximation is used, the numerical solution can only have trailing waves.
(ii) If the 7-point stencil DRP scheme is used, the numerical solution may have both leading and trailing waves. Estimate the wavelength of the leading waves.
4.2. In solving the convective wave equation,
d U d U
—– + C = 0,
d t dx
by approximating the spatial derivative by finite difference quotient and marching the solution in time by the fourth-order RK scheme, it has been shown that the solution, in wave number space, is governed by the equation
4
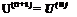1 + ^2 Cj (-icaAt)), j=1
where a(a) is the wave number of the finite difference scheme and n is the time level. One may consider this as a first-order finite difference equation in n (see Chapter 1). Find the exact solution of this finite difference equation. To avoid numerical instability, the absolute value of the characteristic root must be smaller than 1.0. Suppose a is the wave number of the standard sixth-order central difference scheme and Cj’s are the coefficients of the standard fourth-order RK scheme. Determine the largest time step At that may be used without encountering numerical instability.
