Pulse Laser Heating on Thin Metal Film

We consider short-pulse laser heating on a thin metal film to determine the thermal diffusion timescale of TSP applied to the film. The heat conduction equation for this problem is

da

— = aT V2a, (8.28)

dt T

where a = T – Tin is a temperature change of the film from an initial temperature Tn and aT is the thermal diffusivity of the metal film. The Lapalce operator in Eq. (8.28) is defined as V2 = d2 /dr2 + r ]d/dr + d2 /d z2, where r is the radial distance from the center of a hot spot heated by a laser and z is the coordinate normal to the metal film directing from the heated side to other side. The initial temperature Tn is assumed to be the ambient temperature. After heated by a laser pulse, the film is cooled down due to natural convection on both the sides of the metal film. When the surface temperature of the metal film decreases fast enough along the radial direction from the center of the hot spot (i. e., rd 0 as r ^), we introduce a spatially averaging operator

<a> 2 = — Г rd dr, (8.29)

The initial and boundary conditions for Eq. (8.30) are <a>2 (z,0)= 0,

where hc is the average heat transfer coefficient of natural convection, k is the thermal conductivity, S(t) is the Dirac-delta function, nm is the metal film thickness, and Paser represents the strength of the pulse-laser heat source. There are two physical processes involved: rapid heating of the film by the laser pulse and relatively slow cooling process due to natural convection. At the beginning, since the film is heated in a very short time interval, the natural convection terms in the boundary conditions can be neglected; thus, the problem is simplified for the rapid heating process. For a thin metal film (nm << 1), application of the Laplace transform 0(z, s) = La(<Є>2) to Eqs. (8.30) and (8.31) yields

(8.32)

where s is the complex variable in the Laplace transform. The inverse Laplace transform leads to an asymptotic expression for the laser heating when t is small

< в >2 = P‘aseraT erfc(Jt1 /t). (8.33)

кП m

The characteristic timescale for the laser heating is t1 = n2m /(4aT ).

For the slow cooling process due to natural convection after the pulse-laser heat source ceases, we introduce an additional average operator across the metal film

1 rnm

<в>3 =— І <в>2dz. (8.34)

Vm J°

Applying the operator Eq. (8.34) to Eq. (8.30) leads to a simple lumped model for the cooling process

d < в >3 =- < в > 3 +aTpaser S(t). (8.35)

dt dmk k dm

The solution to Eq. (8.35) is

P a

<e> = laser T exp( – 2t/t2) . (8.36)

kn m

Eq. (8.36) describes an exponential decay of the averaged temperature, which gives the characteristic timescale t2 = knm /(2aT hc) for the cooling process due to natural convection.

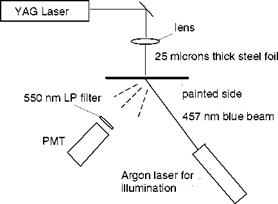
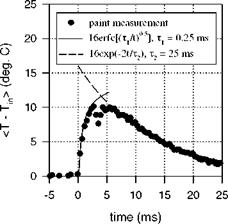
Obviously, for the problem of pulse laser heating on a thin film, there are the fast timescale t1 = nm /(4aT ) and slow timescale t2 = knm /(2aT hc). The time response of Ru(bpy)-Shellac TSP to a rapid temperature rise was tested by utilizing short pulse laser heating on a 25-|jm thick steel film. Figure 8.16 is a schematic of the experimental set-up. One side of the steel film was heated by a pulse laser beam with a 8-ns duration from a Nd:YAG laser (532 nm at an 800-mJ maximum output) through a focusing lens. The opposite side of the steel film was coated with a 10-|jm thick Ru(bpy)-Shellac TSP illuminated by a 457-nm blue beam from a 1-mW Argon laser at the hot spot. The response of the luminescent emission from TSP to pulse laser heating was detected using a PMT, and the signal was acquired using an oscilloscope (Tektronix TDS 420). The surface temperature was calculated from the luminescent intensity using a priori calibration relation for TSP. Figure 8.17 shows a typical transient response of the surface temperature to pulse laser heating on the steel film. The surface
temperature increases rapidly after heating at the film and then decays due to natural convection. To estimate the response times, the asymptotic solutions Eq.

(8.32) and Eq. (8.36) were used to fit the experimental data. The response time of TSP for the laser heating process was t1 = 0.25 ms, while the time constant for the cooling process by natural convection was t2 = 12.5 ms.

532 nm pulse green beam Fig. 8.16. Schematic of a pulse laser heating setup for testing TSP time response. From Liu et al. (1997b)

Fig. 8.17. Temperature response of Ru(bpy)-Shellac TSP to pulse laser heating on a steel foil. From Liu et al. (1997b)