RESPONSE TO GUSTS—RIGID AIRPLANE, PITCHING NEGLECTED

Let us assume, as in § 8.2, (1) that the airplane is initially in horizontal flight at a constant speed U, (2) that the gust is normal to the flight path of the airplane and has a velocity distribution w in the direction of flight and is uniform spanwise, (3) that the variation of the forward speed of the airplane as it traverses the gust can be neglected, and (4) that the gust intensity and the induced motion are so small that the linearized aero­dynamic theory is valid. Whereas in § 8.2 the quasi-steady aerodynamic coefficients are used, we shall now show how the unsteady aerodynamic forces can be taken into account.

The equation of motion of the airplane having one degree of freedom is

mz = — L (1)

where m is the total mass, z the downward displacement, and L the upward lift.

The lift consists of two parts; that arising from the motion of the airplane, and that induced by the gust.

The lift induced by the motion of a two-dimensional airfoil in an incom­pressible fluid has been derived in § 6.7. As in § 6.7, it is convenient to introduce the dimensionless time parameter r: 2

where c denotes the chord length. A dot will indicate a differentiation with respect to the physical time t, whereas a prime will indicate a differ­entiation with respect to r. Thus z — dzjdt, z’ — dzjdr, z = (2 Vjc)z’. According to Eqs. 8 and 9 of § 6.7, we may write the lift induced by an airplane motion which starts at r = 0 as

In the above equation, p is the density of the fluid, S is the wing area, a = dCLjdct. is the steady-state lift curve slope (per radian), and Ф(т) is Wagner’s function. Whereas the equations in § 6.7 are written for a two – dimensional flow of an incompressible fluid, Eq. 3 may be considered applicable to compressible fluids when Ф(т) is properly modified for Mach number. Strip assumption is assumed for the aerodynamic action, and the finite span effect will be corrected in an overall manner by correcting the lift curve slope a for aspect ratio as in a steady flow.

The lift induced by the gust can be expressed by a similar equation, based on a fundamental function T(t), which represents the ratio of the transient lift to the steady-state lift on an airfoil penetrating a sharp-edged gust normal to the flight path. Let the speed of the sharp-edged gust be w; then by definition the transient lift coefficient is

CjJr) = a ~T(t) (4)

where a is the steady-state lift-curve slope, and т is the dimensionless time parameter as before. It is convenient to interpret т here as the distance traveled by the airfoil, measured in semichords.

Tables 10.2 and 10.3 give the approximate expressions of Ф(т) and T"(r) at Mach number zero, obtained by R. T. Jones15-43 for elliptic wings. For T(t) it is assumed that the leading edge of the airfoil en­counters the sharp-edged gust at the instant r — 0.

Table 10.2. Wagner’s Function Ф(т) at M = 0 Ж Ф (t) a 3 1 – 0.283e-°-S4OT 1.27Г 6 1 – 0.361e-°-38lT 1.577 CO 1 – 0.165e-°-04Sr – 0.335°—°-300t 277

Table 10.3. Kiissner’s Function ‘F(t) at M — 0 Ж ‘F(t) а 3 1 – 0.679е~°-558т – 0.227е-3-20т 1.2тг 6 1 – 0.448е~°-290т – 0.272е-°-725т – 0.193<?-3-00т 1.5тг CO 1 – 0.500е-°-130г – 0.500е~г 27т

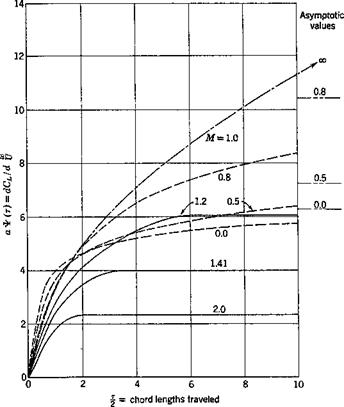
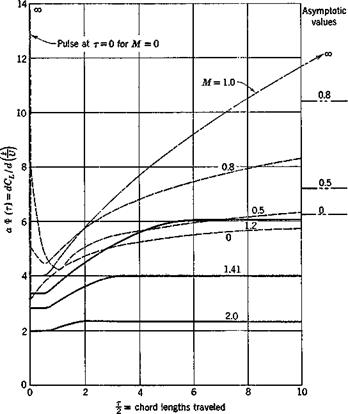
Figure 10.4 shows the results of a linearized theory for the indicial admittance of a two-dimensional airfoil entering a sharp-edged gust. In

Fig. 10.4. Indicial admittance of the lift of a restrained wing to unit sharp – edged gust. Two-dimensional wing for several Mach numbers. From Lomax, Ref. 15.84. (Figure reproduced by courtesy of the NACA.)

order to indicate the effect of compressibility, the ratio dCL/d = аТ(т)

is presented. Figure 10.5 shows the indicial admittance of a two-dimen­sional airfoil to a sudden sinking speed, i. e., ЭСХ/Э = а Ф(т). The

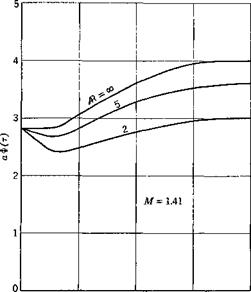
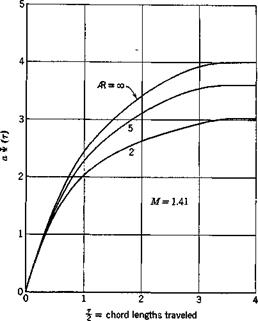
effect of finite-aspect ratio at Mach number 1.41 is shown in Fig. 10.6. These results are given by Lomax.15,84

Fig. 10.5. Indicial admittance of the lift to a sudden sinking speed as a function of chord length traveled. Two-dimensional wing for several Mach numbers. (Figure reproduced by courtesy of the NACA.)

The lift induced by a variable gust can be written as a Duhamel integral. Since Y(0) = 0, we obtain, according to Eq. 27 of § 8,1,

. Ur) = plPSa Ґ ^ – a) da

2 Jo U

0 12 3 4 j = chord lengths traveled

Fig. 10.6. The effect of finite-aspect ratio on аФ(т) and aV(r) at Mach number 1.41. Rectangular wings of aspect ratios 2, 5, and со. (Courtesy of the NACA.)

Again the strip assumption is used here and a is corrected for aspect ratio. The prime over Y’ indicates differentiation with respect to the variable r. The equation of motion of the airplane is therefore

(s + 0.130X5 + l)(s3 + axs2 + + a3) (1 )

where

0.345,m + 0.3363 0.0135,m + 0.1436

^ + 0.25 * "2 ~ 7+^25

0.006825 ’

3 ju + 0.25

z"(t) can be found from Eqs. 13 according to Heaviside’s expansion as demonstrated in § 10.2. From z"(t) the acceleration z in physical units is obtained:

5 = U2 Z"(T) (15)

The maximum acceleration calculated from Eq. 15 is smaller than that given by Eq. 9 of § 8.2, where quasi-steady aerodynamic coefficients are

used. The ratio between the values of the maximum acceleration given by Eq. 15 and Eq. 9 of § 8.2 represents the effect of the lag in time for the circulation to grow after encountering the gust. This ratio can be obtained by dividing smax by the quasi-steady value — (U//tc)w0.

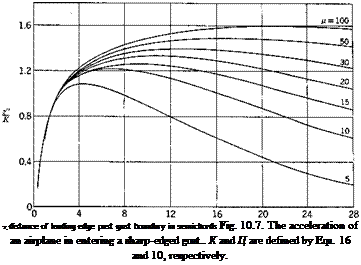
The calculated result of z" in an incompressible fluid, expressed in units of K, where

(16)

is shown in Fig. 10.7. The true value of z" is the value shown in the

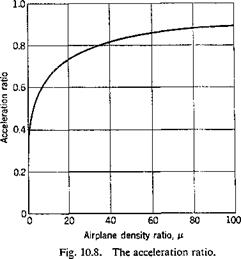
figure times the value of K. The acceleration ratio 2rnax/(maximum quasi­steady acceleration) is shown in Fig. 10.8. The importance of the airplane density ratio ц on the gust-response characteristics of an airplane is evident.

For other gust profiles, we may either use Eq. 9 directly with proper to find the inverse transform, or use the response to a sharp-edged

gust obtained above to generalize by a Duhamel integral. The latter is a more practical procedure.