Torsional Divergence

If it is presumed that the configuration parameters of the uniform wing are known, then it is possible to solve Eq. (4.45) to determine the resulting twist distribution and associated airload. To simplify the notation, let

qcae

~w

1

== (qc2cmac – Nmgd) GJ

so that

Note that X2 and ar are independent of y because the wing is assumed to be uniform. The static-aeroelastic equilibrium equation now can be written as

d26 t

—— + х2в = – X2 (ar + ar) (4.49)

dy2

The general solution to this linear ordinary differential equation is

в = Asin(Xy) + B cos(Xy) – (ar + ar) (4.50)

subject to the condition that X = 0. Applying the boundary conditions, we find that

в (0) = 0: B = ar + ar

в'(£) = 0: A = B tan(X£)

where () = d()/dy. Thus, the elastic-twist distribution becomes в = (ar + ar) [tan(X£) sin(Xy) + cos(Xy) – 1]

Because в is now known, the spanwise-lift distribution can be found using the relationship

L’ = qca(ar + в)

It is important to note from the expression for elastic twist that в becomes infinite as XI approaches n/2. This phenomenon is called “torsional divergence” and depends on the numerical value of

X = M (4’54)

Thus, it is apparent that there exists a value of the dynamic pressure q = qD, at which XI equals n/2, where the elastic twist theoretically becomes infinite. The value qD is called the “divergence dynamic pressure” and is given by

GJ / n 2 qD eca 2£/	(4.55)
Noting now that we can write
x£ = n yq	(4.56)
with
4 § и	(4.57)

the twist angle of the wing at the tip can be written as

в(£) = (ar + ar) [sec(X£) – 1]

= (ar + ar) sec (2^) – 1

q

1.0

0.2 0.4 0.6 0.8

Figure 4.13. Plot of twist angle for the wing tip versus q for ar + ar = 1

where Eq. (4.48) now can be written as

(4.59)

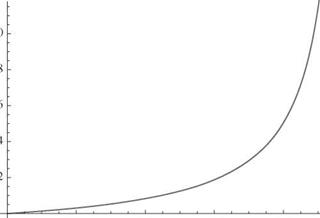
Letting d be zero so that ar becomes independent of q, we can examine the behavior of в (£) versus q. Such a function is plotted in Fig. 4.13, where we see that the tip-twist angle goes to infinity as q approaches unity. Note that the character of the plot in Fig. 4.13 is similar to the prebuckling behavior of columns that have imperfections. It is of practical interest to note that the tip-twist angle may become sufficiently large to warrant concern about the structural integrity for dynamic pressures well below qD. In practice, designers normally require the divergence dynamic pressure to be outside of the vehicle’s flight envelope—perhaps by specifying an appropriate factor of safety.

Because this instability occurs at a dynamic pressure that is independent of the right-hand side of Eq. (4.49), as long as the right-hand side is nonzero, it seems possible that the divergence condition could be obtained from the homogeneous equilibrium equation

(4.60)

The general solution to this eigenvalue problem of the Sturm-Liouville type is

в = Asin(Xy) + B cos(Xy)

for X = 0. Applying the boundary conditions, we obtain

в (0) = 0: B = 0

в ‘(£) = 0: AX cos(X-f) = 0

If A = 0 in the last condition, there is no deflection; this is a so-called trivial solu­tion. Because X = 0, a nontrivial solution is obtained when cos(Xl) = 0. This is the “characteristic equation” with solutions given by

Xnl = (2n – 1) 2 (n = 1, 2,…) (4.63)

These values are called “eigenvalues.” This set of values for Xnl corresponds to a set of dynamic pressures

q=(2n – ч2(Ц)2 G (n=12-o (4-64)

The lowest of these values, q, is equal to the divergence dynamic pressure, qD, pre­viously obtained from the inhomogeneous equilibrium equation. This result implies that there are nontrivial solutions of the homogeneous equation for the elastic twist. In other words, even for cases in which the right-hand side of Eq. (4.49) is zero (i. e., when ar + ar = 0), there is a nontrivial solution

0n = An sin(Xn^) (4.65)

for each of these discrete values of dynamic pressure. Because An is undetermined, the amplitude of en is arbitrary, which means that the effective torsional stiffness is zero whenever the dynamic pressure q = qn. The mode shape в is the divergence mode shape, which must not be confused with the twist distribution obtained from the inhomogeneous equation.

If the elastic axis is upstream of the aerodynamic center, then e < 0 and X is imaginary in the preceding analysis. The characteristic equation for the divergence condition becomes cosh(|X|l) = 0. Because there is no real value of X that satisfies this equation, the divergence phenomenon does not occur in this case.