Flow Past a General Body of Revolution

The approach outlined in Section 7.9 may be extended by distributing increasingly source-sink pairs of finite strength inside the body or along the body axis. The sum of the source and sink strengths must be zero if the body is to be closed. Simple body shapes may be treated in this way; however, solutions for body shapes of practical interest are necessarily numerical in character. If it is required to find the pressure distribution on a suitably slender body of revolution, then an approximate analytical solution may be found that uses source singularities distributed along the body axis. The velocity potential for a uniform flow superposed with a source distributed along the body axis from to x2 is expressed as follows (see Karamcheti, 1967):

(7.37)

where Д£) is the source strength per unit length, /(^)d^ is the infinitesimal source strength at x = x, and the point (x, r) is a field point in cylindrical coordinates as shown in Figure 7.11. The student may verify that this expression for the velocity potential satisfies the Laplace’s Equation. Also, study the derivation of an analogous expression for the stream function that is carried out in Section 7.11.

Using Eq. 7.37 and applying the tangency-boundary condition at the surface of a given body leads to an integral equation for the unknown source-strength distri­bution, /(^). Rather than directly solving this integral equation for the source-strength distribution, it is assumed that the slenderness ratio, e, of the body is small, where e = [(maximum body radius)/(body length)]. For small e, the integral operator con­taining /(^) can be expanded asymptotically in a power series (Wang, et al, 1985). It then may be shown that the source distribution, /(x), as well as the values of x1 and x2, can be related to the axial distribution of the body cross-sectional area, S(x). When these expressions are used in Eq. 7.37, the result is an asymptotic expansion for the velocity potential, which is expressed in terms of a simple geometric property, S(x), of the body. The velocity components on the body surface and, hence, the inviscid- flow pressure distribution follow directly by definition. A similar approach for slender axisymmetric bodies in a supersonic flow is discussed in compressible flow text books.

Figure 7.12 shows the pressure coefficient on the surface of an ellipsoid as evalu­ated by an exact analytical solution and by a numerical solution. Also shown in this figure (i. e., the solid line) is the pressure coefficient as calculated from the approxi­mate velocity potential obtained by using the asymptotic approach discussed previ­ously. Notice that when the body is slender, e = 0.10, the approximate solution agrees

r

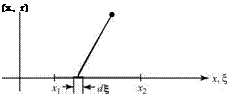Fig. 7.11. Coordinate system and continuous source distribution.

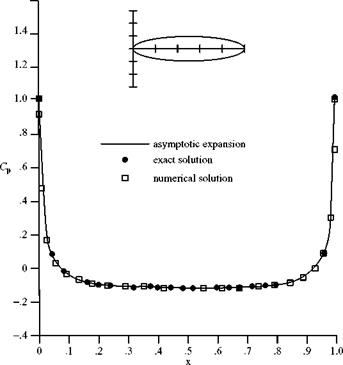
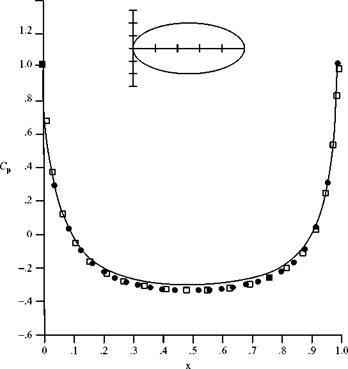
well with the exact result, whereas for a body that is not so slender, e = 0.20, the asymptotic solution does not predict the exact result as well.