FLUTTER

The method of Laplace transformation can be applied to study the stability of oscillating airfoils. Let us consider the motion of a two – dimensional flat-plate airfoil of unit span having two degrees of freedom h and a as considered in § 6.8. The equations of motion are given by Eqs.8,9 and 10 of § 6.8. The Laplace transformation of these equations can be obtained easily. Assuming that

h — h = a = a = 0 when t = 0

we obtain

A(s)^{h/b} + = £Є{Р) /s2

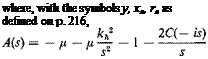D{s)Se{hjb} + E(s)£e{v) = E£{Q) /s2

B(s) — — yxa -(- ah

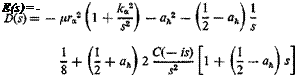s

The function C(— is)/s denotes the Laplace transform of the Wagner’s function Ф(т):

A comparison of this equation with Eq. 6 of § 6.9 shows that C(— is) can be obtained from the Theodorsen’s function C(k) by replacing к by — is. From the form of Theodorsen’s function given in Eqs. 8, 8a, 8b of § 6.9, it is clear that C(k) as a function of the complex variable к is analytic in the entire upper half-plane, including the real axis. Correspondingly C(— is) is analytic for the right half-plane R1 j > 0. In other words, if we put ik = s, then the expressions of lift and moment given in Eqs. 9 of § 6.9 hold for a divergent oscillation e3T, (R1 j > 0). The validity of this generalization has been discussed by W. P. Jones15’80 and Van de Vooren in his discussion of Ref. 15.26.

The solution of Eq. 2 may be written as*

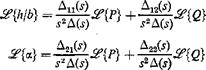(5)

where

Д11 — E, Д]д — В, Д si — D, Д22 — A (6)

AO) = A(s) B(s)

D(s) E(s)

The functions ДО), ДпО), • • •, Д220) have no poles in the right half­plane, R1 s > 0. Hence, in the right half-plane, the poles of £E{hjb}, etc., if any, must arise from the zeros of ДО), provided that?{P} and.!E{Q has no poles on the right half-plane. If ДО) has a root with a positive real part, the motion h and a will eventually become infinitely large. If Д0) has no root with a positive real part, the motion will be convergent. Hence, the stability question is reduced to an investigation of the zeros of ДО) in the right half-plane, f

Dugundji10,9 uses the Nyquist diagram for this purpose. It is necessary to examine the number of times the curve of ДО) encircles the origin as s traces an infinite semicircle on the right half-plane (Fig. 10.16) in the counterclockwise direction. Along the imaginary axis, j = ik, ДО)

* The functions An(j)/A(j), An(s)/A(s), etc., are proportional to the transfer functions. From the general interpretation of the transfer functions it is clear that, if s is replaced by ik, then An(ik)IA(ik), etc., represent the admittance of the dynamical system to

reduces into A(ik), which is exactly the flutter determinant A as given in Eq. 18, § 6.9. Along the semicircle, j = Rel6, ^ ~ ^ ^ б < ^ j

lim C(- is) -> $ (8)

R—»-co

which can be easily seen from Eqs. 8a, 8b of § 6.9 or deduced from the asymptotic expansion of the Hankel functions in Eq. 8, § 6.9. Therefore A(s’) tends to a constant on the semicircle as R -> со:

— (/M + 1) — a

lim A(j) -*■

и-"* — fixa + a — [irf — a[29] [30] [31] [32] —-

At the origin, s = 0, Eqs. 3, 7 show that A(^) has a pole of order four. The contour of mapping must be deformed by describing a small semi­circle from ei to — si on the right half-plane. The corresponding change in the phase angle of A(s) is 477.

The mapping of A(s) can now be made without difficulty. When j = ik, the real and imaginary part of A {ik) can be computed from Eq. 19, § 6.9. Note that A (ik) need be calculated for positive values of к only. Let C(k) denote the complex conjugate of C(k), then we have

C(- k) = C(k) (10)

i. e.

as t -*■ со.

C(k) = F + iG, C(- k) — F — iG

This is obvious from the definition of C{k) given in Eq. 6 of § 6.9, by re­placing к by — k, і by — i. It can also be seen from Eqs. 8, § 6.9. So

Д(- ik) = A(ik)

The mapping of the negative imaginary axis is just the mirror image in the real axis of that of the positive imaginary axis.

Example. Consider a wing with the following physical parameters:

Ц — 10, ak == — 0.2, xx — 0.1, л*2 = |-

coJcoa = b = 6/27T = 0.9549 ft, t»a = 12 cycles per second

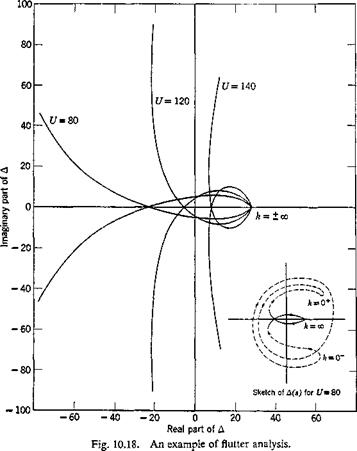
The map of the semicircle on the A(j) plane is sketched in Fig. 10.18. It is clearly seen that, for the cases U = 80 and 120 ft per sec, the curve

encircles the origin once in the positive direction and once in the negative direction. The net encirclement is zero. Hence, the motion is stable. In case U = 140 ft per sec, the curve encircles the origin twice in the positive direction. Hence, A(.s) has two zeros with positive real part. The wing is unstable at U — 140. An examination based on the method of § 6.9 shows that the critical flutter speed is 129 ft per sec.

The difference between the present analysis and that in § 6.9 is that, whereas in § 6.9 the equation Д = 0 is to be solved for a pair of roots kCI and UCI, in the present analysis the values of the flutter determinant Д are examined as к varies from — oo to со.

The present method has a definite advantage when the flutter speed is so high that the effect of compressibility becomes important. As the contours are calculated for each specified speed U, the Mach number is known and the appropriate aerodynamic coefficients can be obtained directly from existing tables. Hence, the result of each calculation is a positive statement about the stability of the system, and the iterative correction for the Mach number effect is unnecessary.