FUNCTIONAL DIAGRAMS

In analyzing an aeroelastic system, it is convenient to distinguish the various functions that each element performs. Sometimes many elements together perform a single function, such as an electronic amplifier, which converts an input signal into another signal, but is composed of many resistors, capacitors, transformers, and vacuum tubes. Sometimes a single element performs several functions, such as an airplane wing, which produces lift force, elastic deformation, and inertia force. Whether several elements should be grouped together to be considered as a single

unit or a single element should be analyzed into several functional units depends on. the particular problem under consideration. But in all cases it is helpful to represent the entire system in a pictorial form so that the interaction among various elements can be clearly seen. Such pictorial representations are called functional diagrams. They are also called block diagrams if no single physical element is analyzed into several functional units.

The meaning of functional diagrams can be best illustrated by examples.

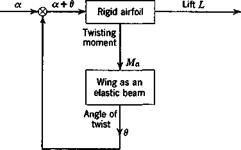
Lift of an Elastic Wing. If a change of angle of attack a (measured at the wing root) of a cantilever wing is regarded as an input, and the total

FTg. 11.1. Functional diagram of a wing.

lift force L acting on the wing as an output, the function of the wing may be represented symbolically as in Fig. 11.1. The relation between L and a, however, depends on the elastic deformation of the wing. It is convenient to consider the wing as composed of two elements: the wing as a lift-producing mechanism, and the wing as an elastic structure. With respect to aerodynamics, each configuration of the wing may be con­sidered as rigid. With respect to the elastic deformation, the action of

Fig. 11.2. An elastic wing.

aerodynamic forces is the same as any other system of exterior forces. The partial problems in aerodynamics and elasticity may be solved in the classical manner, but these two solutions must be properly combined to account for the behavior of an elastic wing. An elastic wing may be represented functionally as in Fig. 11.2. The airfoil, at an angle of attack a and having a deflection surface в, produces an aerodynamic pressure distribution p. The elastic wing, in response to the pressure distribution, produces a deflection surface в. Let us denote the wing surface corres­ponding to the initial angle of attack a also by the symbol a; then the

geometrical configuration may be simply written as a + 0, with respect to which the aerodynamic force is computed. Thus the rigid-airfoil-elastic – structure system forms a loop. It is a feedback system.

Wing Divergence. In the preceding example let a and 0 be so measured that L = 0 when a = 0 = 0. Then, in general, 0 = 0 is the only solution

JL Ma

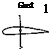when a = 0. Let us now ask whether there exists a nontrivial solution 0 Ф 0 when a = 0 (Fig. 11.3). If such a solution exists, the wing is said to be critically divergent. In the critical divergent condition the amplitude of 0 is indeterminate. Since the system represented in Fig. 11.3 can be superposed on that in Fig. 11.2, it is clear that, at the critical-divergent condition, the lift problem has no unique solution. Conversely, when the

wing is nondivergent, the unique solution of Fig. 11.3 is 0 = 0, and the corresponding solution of Fig. 11.2 exists.

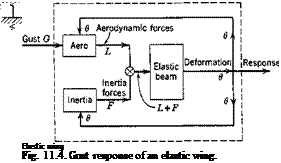
Gust Loading on an Airfoil. In dynamic problems the wing performs three distinct functions: It produces (1) aerodynamic force, (2) inertia force, (3) elastic deformation. It is convenient to represent the wing’s triple functions as three independent operators. In an example of the gust loading on a wing which is restrained against pitching, the functional diagram may be shown in Fig. 11.4.

Flutter is a companion problem. Instead of finding the response of
the wing to a gust, we ask whether the homogeneous system obtained by setting G = 0 in Fig. 11.4, has a nontrivial solution.

Again, as in the corresponding problems of lift and divergence, here the alternative theorem is: Either the homogeneous system has a nontrivial solution (flutter occurs), or the gust-response problem has a solution.