Navier-Stokes Equations

The differential-momentum equations that include viscous terms are called the Navier-Stokes equations. Recall from Chapter 3 that the differential-momentum equation can be derived by applying the Conservation of Momentum principle (in the form of Newton’s Second Law) to a moving fluid particle. The result for two­dimensional viscous flow was Eq. 3.74. Here again, we begin by applying Newton’s Second Law to a fluid particle in Cartesian coordinates; however, the viscous forces now must be accounted for in detail. For convenience, the fluid particle is assumed to be a cube with volume (dxdydz). Because the fluid particle is of constant mass p(dxdydz):

D [p(dxdydz)V] = p(dxdydz) = f,

where DV/Dt for steady flow is the convective acceleration of the particle and F is the net force acting on the fluid particle.

where the right side is written as differential-force components because we are dealing with an infinitesimal fluid particle. It remains to detail the force terms on the right side of this equation. In the absence of body forces, these terms express forces (or stresses) exerted on the outside surfaces of the fluid particle by the surroundings. Recall that in addition to normal pressure forces (i. e., the only forces present in an inviscid flow), the force terms in Eq. 8.5 must include all of the shear and normal forces due to the presence of viscosity.

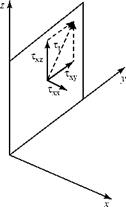
For convenience, the fluid-particle cube with volume dxdydz is assumed to be at the origin of coordinates in a snapshot of the moving particle taken at an instant of time, as shown in Fig. 8.2. In general, the surface stress, t, is at an angle with res­pect to each surface of the cube, as illustrated in the figure for the surface passing through the origin and perpendicular to the x-axis. Now, we decompose this general surface stress, t, into a component normal to the face, Tn, and a component tan­gential to the face, Tt. The component Tt can be decomposed further into two com­ponents in the coordinate directions, as shown in Fig. 8.3, where Txx = Tn.

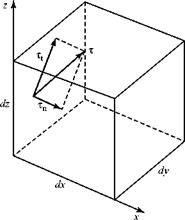
Figure 8.2. Differential element and general stress.

The following notation is used:

1. The first subscript on the symbol for stress indicates the axis normal to the plane on which the stress acts.

2. The second subscript corresponds to the direction in which the stress acts.

Thus, Txz indicates the stress on a plane normal to the x-axis and acting in the z-direction. Figures similar to Fig. 8.3 may be drawn for the five other planes that define the fluid particle. Fig. 8.4 indicates all of the stresses acting in the x-direction on the six faces of the fluid particle. For convenience, baseline values of the stresses are assigned to the faces in the coordinate planes. Thus, the tangential stress on the rear surface is given by:

As a matter of convention, the stresses on a plane are taken to be the force per unit area acting on the side of the plane that faces in the positive coordinate direction. Stresses acting on the outside surfaces of the element are shown with a dot • on the arrow in Fig. 8.4. Thus, the stress on the upper surface of the fluid element acts on the outside of the element in Fig. 8.4, whereas the shear stress on the lower surface acts on the inside of the surface. Likewise, Txx is a normal stress acting on the inside of

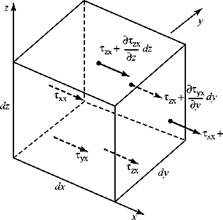Figure 8.4. Stresses acting on a fluid element.

the left face of the element in Fig. 8.4; hence, – t^ is a normal stress acting on the out­side of the left face of the element. Notice how this convention returns the familiar result in the case of inviscid flow. In that case, Txx = – p (see Eq. 8.13), and the normal pressure force acts toward the right on the outside of the left face and toward the left on the outside of the right face of the element. Thus, the pressure force acts on the fluid particle, as our formulation of the momentum-balance equation requires.

Using this notation and convention and taking a force (i. e., stress times area) to be positive in the positive coordinate direction, the net force acting on the element in the x-direction (for example) can be deduced. Recall that Newton’s Second Law requires this to be the net force acting on the element. Remember that a force acting on the inside of a surface represents the force of the element acting on the surround­ings, so that the direction of this force must be reversed before it is entered into the expression for Newton’s Second Law. The net force acting on the outside surfaces of the particle, Fig. 8.4, in the x-direction is then as follows:

or, canceling:

and

Notice that Eqs. 8.6b and 8.6c can be obtained directly from Eq. 8.6a by permuting the second subscript because this is the direction subscript. Also notice that dxdydz is simply the volume of the fluid particle.

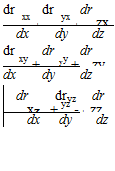Finally, we substitute Eq. 8.6 for the force terms on the right side of Eq. 8.5. Then, we cancel the coefficient (dxdydz) on both sides of the equation. This implies that the resulting equation is independent of the volume of the fluid particle, which is expected. The result is:

x

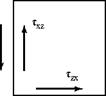
These are the components of the momentum equation in three-dimensional Car­tesian coordinates. Notice that even with the help of the continuity equation, there are many more unknowns than there are equations. The fluid stresses on the right side of Eq. 8.7 must be studied further, with the aim of expressing them in terms of velocity-component derivatives. Recall that in these equations, the normal stresses (with the double subscript) consist of both pressure and viscous stresses. The mixed subscripts xy, zx, and so on denote shear (i. e., tangential) stresses. The problem of the large number of unknowns in Eq. 8.7 is alleviated by realizing that the shear stresses are not independent. Consider the tangential stresses acting on the two­dimensional fluid element in Fig. 8.5.

The tangential stresses acting on the outside faces of the fluid element are shown. If the torque about the Point 0 is not zero, the nonzero torque causes an infinite angular acceleration of the fluid element because it has infinitesimal mass. Because this cannot occur in nature, the tangential stresses must be in equilibrium such that:

Txz _ Tzx, (8.8a)

and, by a similar argument:

Txy _ Tyx; Tyz _ Tzy, (8.8b)

This reduces the number of unknown stresses to six: three shear stresses and three normal stresses. All of these viscous stresses can be related to velocity-component derivatives. How this is accomplished is discussed in two parts.

1. Shear stress. The molecular origins of shear stress are discussed in Chapter 2. Recall that in solid mechanics, the shear stress on a solid is proportional to the strain or angular distortion (i. e., Hooke’s Law). For liquid or gases, it is assumed that the shear stress is proportional to the strain rate, or to the rate of change of angular distortion of the fluid element. For air and water, this assumption has been well validated by experiment. The proportionality between shear stress and strain rate is linear for air and water; hence, they are termed Newtonian fluids. If there is a nonlinear dependence between shear stress and strain rate (e. g., as in blood), then the fluid is termed non-Newtonian. Only Newtonian fluids are considered here.

In Chapter 4, the concept of the strain of a fluid element is discussed. The rate of strain, exy, of a two-dimensional, fluid particle in the x-y plane was defined

in terms of the rate of change of angular distortion of the particle and then in terms of velocity-component derivatives, Eq. 4.3. This result in Chapter 4 was set aside for later use and is used now. Rewriting Eq. 4.3:

_ dv du £xy ~dx + dy ‘

For a Newtonian fluid, it is assumed that Txy ~ exy or Txy stant of proportionality. Thus,

The constant of proportionality, p, in Eqs. (8.10a, b,c) is called the coefficient of viscosity, and is termed a transport property of the fluid. It has different values for different fluids. The magnitude of the coefficient of viscosity may be thought of physically as being a measure of the ability of a gas/liquid to resist shear defor­mations. Since shear stress in a gas/liquid arises from molecular interactions, as discussed in Chapter 2, it may be shown from kinetic theory that the coefficient of viscosity is a function of pressure and temperature. For typical aerodynamic problems the pressure levels are such that the small pressure dependence may be ignored. Thus, viscosity may be assumed to be a function of temperature only. For incompressible flow, where any temperature excursion in the flow is very small, the coefficient of viscosity may be taken to be a constant. For air at stan­dard temperature,

M _ 3.72.10-7 slug/fts (m _ 1.78.10-5 kg/ms). (8.11)

Because the ratio р/р appears often in the analysis, it is given a special symbol and name, v _ р/р, the kinematic viscosity. At standard conditions, the kinematic viscosity of air has the value:

v _ 1.55.10-4 ft2/ s (1.44.10-5 m2/s).

In some applications, involving flows with large temperature variations may be necessary to account for the variations of the viscosity with temperature. For such cases, we use results from kinetic theory, such as Sutherland’s Law:

where for air:

T0 = 491.76° R (T0 _ 273.2° K)

< рb = 3.58540-7 slug/fts (pb _ 1.716.10-5kg/ms)

S = 199.8° R (5 = 111°*:).

For temperatures between 378 and 3,420° R, this expression gives values within 2 percent of the experimentally measured values. The viscosity coefficient and other physical parameters also may vary with pressure. Values of the viscosity coefficients and parameters for other gases and liquids are in Thwaites, 1949 and Hiemenz, 1911. For problems involving incompressible flow, constant values for the viscosity coefficient (e. g., those given in Eq. 8.11) are appropriate.

2. Normal Stress. In an inviscid flow, the only normal stress on a fluid particle is the pressure. The molecular origin of this pressure is discussed in Chapter 2. However, in a viscous flow, there are normal stresses present in addition to the familiar pressure stresses. This fact is emphasized by introducing the following notation:

x = —p + o

yy и yy

This representation indicates that the normal stress is the sum of two parts: the part due to pressure, p (the negative sign indicates that it acts inward on the particle surface), and a second part, o, which represents normal stresses caused by viscosity. These viscous normal stresses can be significant if there are large velocity gradients du/dx, du/dy, and du/dz at the faces of the fluid particle. These effects often are neglected in aerodynamic applications because the shearing stresses are far more important.

Previously, from a macroscopic viewpoint, we described a fluid particle as being of fixed identity. However, at the molecular level, the actual particles that com­prise the fluid particle are changing continually. Because of the random motion of the molecules, some are leaving the fluid particle and others are entering. Thus, there is a continual diffusion of mass and momentum (at the molecular level) in and out through the surfaces of the particle. If there are rapid inward or outward movements of the faces of the fluid particle, this results in an unbalance of the mol­ecular diffusion of momentum across the particle boundaries in the normal direc­tions. By Newton’s Second Law, there must be a corresponding unbalanced force. It is this force that is denoted as oxx, oyy, and ozz, the normal stresses due to viscosity. Recall that the existence of a shear stress also is explained at the molecular level (see Chapter 2).

The derivation of the defining equations for the viscous normal stresses is pre­sented in detail in Ref. 5. Here, we simply display the results for completeness:

These viscous, normal-stress expressions contain two constants of proportionality. The constant p is the same coefficient of viscosity observed before in the shear-stress expressions. The second constant, X, is called the coefficient of bulk viscosity because it is associated with a change in particle volume. For an incompressible flow, the quantity in square brackets in Eq. 8.14 is zero by virtue of continuity, so that X does not enter into consideration of an incompressible-flow problem.

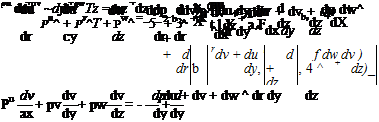It remains to substitute the expressions for the shear stresses in Eq. 8.10 and the normal stresses in Eqs. 8.13 and 8.14 into the appropriate force terms in the momentum expression, Eq. 8.7. The result is:

+ + d du + dw л d dw + dv ^ dr b ydz dr y > b ,dy dz

These are the Navier-Stokes equations for a steady, compressible, three-dimensional, viscous flow.

Notice in Eq. 8.15 that the viscosity coefficients are located inside the spatial derivative. In a compressible flow, the temperature may change greatly over the flow field; hence, the temperature-dependent viscosity coefficients cannot be treated as constants. Recall that derivatives of density (i. e., p, mass per unit volume) do not appear in Eq. 8.15 even for a compressible flow. This is because the mass of the fluid particle, pdrdydz, is constant so that the mass term passes through the Eulerian derivative in the statement of Newton’s Second Law. The volume of the fluid particle then divides out, leaving the density as a coefficient of the substantial derivative.