Navier-Stokes Equations for Incompressible Flow

The Navier-Stokes equations for an incompressible, viscous flow may be written by simplifying Eq. 8.15. As mentioned herein, the terms containing the bulk viscosity, X, drop out when considering an incompressible flow because the continuity equation requires that:

^ + ^ + ^ = 0. (8.16) dr dy dz

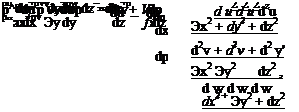Also, the coefficient of viscosity, ц, may be treated as a constant because tempera­ture variations throughout the flow are very small. Thus,

These are the Navier-Stokes equations for steady, incompressible, viscous, three-dimensional flow. Notice that there are now four equations: the continuity equation, Eq. 8.16, written for an incompressible flow; and the three momentum equations in Eq. 8.17. Thus, there are four unknowns: u, v, w, and p. The density, p, is a known constant and the coefficient is viscosity, ц, is a known constant for a particular fluid.

Eq. 8.16 now is written for two-dimensional flow in the x-z (or airfoil) plane. Thus, v = d/dy = 0 and Eq. 8.17 reduces to:

where V2 is the Laplacian operator. These are the Navier-Stokes equations for a steady, two-dimensional, incompressible, viscous flow. Rewriting the continuity equation, Eq. 8.16, for two-dimensional incompressible flow:

^ + ?w = 0. (8.19)

dx dz

This provides the third equation needed to determine the three unknowns, u, w, and p. Carefully examine Eq. 8.18. Note that even after the considerable simpli­fication of assuming an incompressible flow, the Navier-Stokes equations still are nonlinear due to the convective acceleration terms on the left side involving prod­ucts of the velocity components and their derivatives. We cannot use the powerful superposition principle that is a benefit in linear problems. There exist no general methods for integrating these equations, although exact analytical solutions exist for a few special cases that we examine carefully in subsequent sections. This sug­gests that simplifying assumptions must be applied if solutions to viscous problems are to be found. An important simplification takes advantage of the thinness of the usual viscous region, or boundary layer. The Navier-Stokes equations are found to be considerably simpler for the case of a thin boundary layer, but the resulting boundary-layer equations are still nonlinear. Before the boundary-layer equations are developed, it is useful to examine the proper boundary conditions for a viscous – flow problem.