Solution for the general case
The solution of the boundary-layer equations for the flat plate described in Section 7.3.4 is a very special case. Although other similarity solutions exist (i. e. cases where the boundary-layer equations reduce to an ordinary differential equation), they are of limited practical value. In general, it is necessary to solve Eqns (7.7) and (7.14) or, equivalently Eqn (7.29), as partial differential equations.
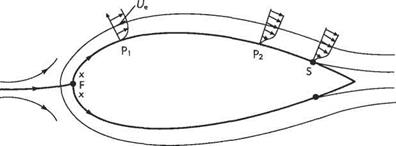
To fix ideas, consider the flow over an aerofoil, as shown in Fig. 7.12. Note that the boundary-layer thickness is greatly exaggerated. The first step is to determine the potential flow around the aerofoil. This would be done computationally by using the panel method described in Section 3.6 for non-lifting aerofoils or Section 4.10 in the case where lift is generated. From this solution for the potential flow the velocity Ue along the surface of the aerofoil can be determined. This will be assumed to be the velocity at the edge of the boundary layer. The location of the fore stagnation point F can also be determined from the solution for Ue. Plainly it corresponds to Ue = 0. (For the non-lifting case of a symmetric aerofoil at zero angle of attack the location of the fore stagnation point will be known in advance from symmetry). This point corresponds to x = 0. And the development of the boundary layers over the top and bottom of the aerofoil have to be calculated separately, unless they are identical, as in symmetric aerofoils at zero incidence.
Mathematically, the boundary-layer equations are parabolic. This means that their solution (i. e. the boundary-layer velocity profile) at an arbitrary point P[, say, (where x = xi) on the aerofoil depends only on the solutions upstream, i. e. at x < X[. This property allows special efficient numerical methods to be used whereby one begins with the solution at the fore stagnation point and marches step by step around the aerofoil, solving the boundary-layer equations at each value of x in turn. This is very much easier than solving the Navier-Stokes equations that in subsonic steady flow are elliptic equations like the Laplace equation. The term elliptic implies that the solution (i. e. the velocity field) at a particular point depends on the solutions at all other points. For elliptic equations the flow field upstream does depend on conditions downstream. How else would the flow approaching the aerofoil sense its presence and begin gradually to deflect from uniform flow in order to flow smoothly
|
around the aerofoil? Nevertheless, numerical solution of the boundary-layer equations is not particularly simple. In order to avoid numerical instability, so-called implicit methods are usually required. These are largely beyond the scope of the present book, but are described in a simple treatment given below in Section 7.11.3.
For aerofoils and other bodies with rounded leading edges, the stagnation flow field determined in Section 2.10.3 gives the initial boundary-layer velocity profile in the vicinity of. v = 0. The velocity Ue along the edge of the boundary layer increases rapidly away from the fore stagnation point, F. The evolving velocity profile in the boundary layer is found by solving the boundary-layer equations step by step by ‘marching’ around the surface of the aerofoil. At some point i/e will reach a maximum at the point of minimum pressure. From this point onwards the pressure gradient along the surface will change sign to become adverse and begin to slow down the boundary-layer flow (as explained above in Section 7.2.6 and below in Section 7.4). A point of inflexion develops in the velocity profile (e. g. at point P2 in Fig. 7.12, see also Fig. 7.6) that moves towards the wall as. x increases. Eventually, the inflexion point reaches the wall itself, the shear stress at the wall falls to zero, reverse flow occurs (see Fig. 7.6), and the boundary layer separates from the surface of the aerofoil at point S. The boundary-layer equations cease to be valid just before separation (where rw = p(du/dy)w = 0) and the calculation is terminated.
Overall the same procedure’s are involved when using the approximate methods described in Section 7.11 below. There a more detailed account of the computation of the boundary layer around an aerofoil will be presented.