Viscous Incompressible Flow

External aerodynamics was a disturbingly mysterious subject before Prandtl solved the mystery with his work on boundary layer theory from 1904 onwards.

L. Rosenhead Laminar Boundary Layers, Oxford 1963

8.1 Introduction

This chapter examines the role of viscosity in the flow of fluids and gases. Although the viscosity of air is small, it must be included in a flow model if we are to explain wing stall and frictional drag, for example. The four preceding chapters are con­cerned with the analysis of airfoils, wings, and bodies of revolution based on an assumption of inviscid flow (i. e., negligible viscous effects). The inviscid-flow model allowed analytical solutions to be developed for predicting, with satisfactory accu­racy, the pressure distribution on bodies of small-thickness ratio at a modest (or zero) angle of attack. However, the inviscid-flow model leads to results that are at odds with experience, such as the prediction that the drag of two-dimensional air­foils and right-circular cylinders is zero. This contradiction is resolved by realizing that actual flows exhibit viscous effects.

Viscosity is discussed from a physical viewpoint in Chapter 2. In Chapters 5, 6, and 7, the existence of viscosity is acknowledged when it is necessary to advance an analytical derivation for an inviscid flow. Also, viscous effects are called on, with words like viscous drag and separation, when comparing the predicted and observed behavior of airfoils and wings. However, no analysis in this textbook has been developed thus far that provides the required detailed physical basis for these effects.

The focus of this chapter is a detailed study of the role of viscosity in an incom­pressible flow, particularly regarding modifications to the behavior of airfoils and wings that was predicted based on an inviscid-flow model. This study answers ques­tions such as: Why does a wing stall? How can stall be predicted or prevented? How is frictional drag on a vehicle calculated?

When we include detailed viscous (and, later, heat-transfer) terms in the con­servation equations of Chapter 3, it leads to a set of equations that defy analytical

Figure 8.1. Typical velocity profile in a boundary layer.

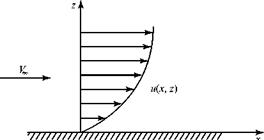solution—even for incompressible flows—except in special cases. In 1904, Prandtl* showed that a very thin “boundary layer” exists on the surface of bodies immersed in a flowing medium that has a small coefficient of viscosity (e. g., air). Within the boundary layer, flow-velocity gradients are large, whereas outside of the boundary layer, they usually are small (Fig. 8.1). Recall from Chapter 2 the argument at the molecular level that the velocity at the wall must be zero. This is termed the no-slip boundary condition.

Recall also from Chapter 2 that the velocity changes from the freestream value are the net result of mixing at the molecular level. This mixing leads to a shear stress in the fluid. Shear stress in a flow is proportional to velocity gradient, as discussed later. Thus, within the thin boundary layer, shear forces dominate, whereas outside of the boundary layer, inertial forces (due to directed motion of the fluid particles) dominate. This allows the problem of flow around a vehicle to be decomposed into two parts, both of which are treated simply by approximate equations appropriate to either an external inviscid flow or a thin viscous boundary layer.

Because the boundary layer is thin, the problem of flow around a vehicle first is treated as if there were no boundary layer present (i. e., inviscid-flow model). Problems in which the viscous layer is not thin (e. g., airfoils beyond the stall) are excluded. The boundary-layer problem is solved next, and then the two solutions are synthesized (i. e., combined) to describe the entire flow field. The pressure distribution arising from the external-flow solution is used as a known in the bound­ary-layer solution, as shown later. Iterations are carried out to account for the small modification to the body shape caused by the presence of the boundary layer.

Alternatively, numerical finite-difference (i. e., CFD) solutions have been devel­oped that can treat the entire flow field in one unified manner and the external flow and the boundary-layer flow need not be decomposed. Such CFD solutions are complex and make strong demands on computer capability. The CFD methods are numerous and the mathematical theory is beyond the scope of this textbook, but we use the simpler concepts to demonstrate the power of such methods and to obtain useful solutions. We begin here by examining many simpler analyses to introduce several concepts that are applicable to all viscous flows.

For streamlined bodies in an incompressible flow, boundary-layer behavior depends on the value of a nondimensional parameter Re, the Reynolds number, which was introduced in Chapter 2:

Re = £Yk, (8.1)

M

Ludwig Prandtl (1875-1953) was a German professor of applied mechanics whose concept of the boundary layer was a breakthrough in the study of viscous flow.

where p is the density, V is the velocity, ц is the coefficient of viscosity, and L is a characteristic length such as a wing chord. This ratio was described in a discussion of similarity parameters, Eq. 2.20. The Re number usually is evaluated at a con­venient reference condition such as the freestream, and it is the most important parameter that influences the characteristics of any viscous flow. If the flow problem involves compressibility, then an additional parameter—the Mach number—must be accounted for in the mathematical modeling.

If all of the streamlines in the flow within the boundary layer are parallel to one another, the boundary-layer flow is said to be in laminas, or to be laminar. In this case, momentum is transported normal to the lamina only by molecular diffusion. If the flow within the boundary layer has a random structure and contains large eddies, then the boundary layer is said to be turbulent. In the turbulent case, momentum is carried across streamlines by convective effects resulting from random fluctu­ations of the fluid. Laminar and turbulent boundary layers each have distinctive properties and methods of solution. Both types are discussed in this chapter.

Both analytical and numerical solutions to incompressible viscous-flow prob­lems are discussed herein. These solutions primarily apply to boundary-layer flows and lead to methods for predicting the following characteristics of an incompressible boundary layer:

1. Profile. The shape of the velocity profile within the boundary layer, from the sur­face of the body to the edge of the layer, must be determined. Knowledge of this profile shape then allows the prediction of skin friction and, thus, frictional drag of a flight vehicle.

2. Growth. The boundary-layer thickness increases with increasing downstream dis­tance along a vehicle surface. The rate of growth of the boundary layer must be found if, for example, it is desired to locate an engine inlet near a vehicle surface but out of the boundary layer so as to avoid ingesting nonuniform boundary-layer flow into the engine. This “growth” may be negative in regions of highly acceler­ated flow.

3. Separation. Under certain circumstances, the flow in the boundary layer leaves the body, or separates. When this occurs, the apparent shape of the body, as seen by the oncoming flow, changes dramatically and the oncoming flow no longer per­ceives a streamlined body. This may have drastic consequences (e. g., wing stall); thus, it is important to determine which parameters influence separation and how separation effects can be minimized or avoided. Separation occurs primarily when the flow is decelerating.

4. Transition. * A boundary layer usually starts to develop at the leading edge of a body as a laminar boundary layer. Farther downstream, it may begin to “tran­sition” into a turbulent profile. This does not occur instantaneously but rather over a streamwise distance. Because turbulent boundary layers cause higher skin friction (and heat transfer) than laminar boundary layers in the same external conditions, it is important that designers have knowledge that allows prediction of the transition location, as well as an understanding of how to delay or prevent transition.

* This term is often confused with separation. It is important that the student clearly understands the meaning of these two terms.

The chapter begins by detailing the viscous terms in the Conservation of Momentum equations (see Chapter 3), which were written in symbolic form when the equations were derived originally. The momentum equations, with all of the vis­cous terms specified, are called the Navier-Stokes equations[25]. Following a discussion of the no-slip boundary condition, exact solutions of the Navier-Stokes equations for incompressible flow are reviewed. Unfortunately, the practical application of these solutions is severely limited, so approximate equations (i. e., the boundary – layer equations) are derived next.

Analytical and numerical (i. e., CFD) solutions to these laminar boundary-layer equations are carried out assuming incompressible flow. These solutions then are examined to interpret the observed behavior of airfoils and wings. Finally, tran­sition of the boundary layer from laminar to turbulent is discussed, and turbulence is introduced. The steady flow of an incompressible fluid with negligible body forces is assumed throughout the discussion.

There is no need to discuss anything further regarding the continuity equation because it contains no force (i. e., viscous) terms. Thus, the continuity equation is the same whether the flow is assumed to be inviscid or viscous. The differential con­tinuity equation was developed in Cartesian coordinates as Eq. 3.53, which for a steady, incompressible flow is:

du dv dw _ ,0

tt – + t – + ^- = 0, (8.2)

dx dy dz

where the local velocity components are u, v, w.

In an incompressible viscous or inviscid flow, the variations in density and tem­perature are so small that the energy (and state) equations may be set aside (i. e., uncoupled). Thus, solutions are sought here for a set of partial-differential equations consisting only of the continuity and momentum equations.