Aeroelastic Analysis of a Typical Section

In this section, we demonstrate the flutter analysis of a linear aeroelastic system. To do this, a simple model is needed. In the older literature on aeroelasticity, flutter analyses often were performed using simple, spring-restrained, rigid-wing models such as the one shown in Fig. 5.2. These were called “typical-section models” and are still appealing because of their physical simplicity. This configuration could represent the case of a rigid, two-dimensional wind-tunnel model that is elastically mounted in a wind-tunnel test section, or it could correspond to a typical airfoil section along a finite wing. In the latter case, the discrete springs would reflect the wing structural bending and torsional stiffnesses, and the reference point would represent the elastic axis.

Of interest in such models are points P, C, Q, and T, which refer, respectively, to the reference point (i. e., where the plunge displacement h is measured), the center of mass, the aerodynamic center (i. e., presumed to be the quarter-chord in subsonic thin-airfoil theory), and the three-quarter-chord (i. e., an important chordwise loca­tion in thin-airfoil theory). The dimensionless parameters e and a (i. e., -1 < e < 1 and -1 < a < 1) determine the locations of the points C and P: when these parame­ters are zero, the points lie on the mid-chord, and when they are positive (negative), the points lie toward the trailing (leading) edge. In the literature, the chordwise
offset of the center of mass from the reference point often appears in the equations of motion. It is typically made dimensionless by the airfoil semi-chord b and denoted by xe = e – a. This so-called static-unbalance parameter is positive when the center of mass is toward the trailing edge from the reference point. The rigid plunging and pitching of the model is restrained by light, linear springs with spring constants kh and k.

It is convenient to formulate the equations of motion from Lagrange’s equa­tions. To do this, we need kinetic and potential energies, as well as the generalized forces resulting from aerodynamic loading. We immediately can write the potential

energy as

1 9 1 9

P = 2 khh2 + 2 kee2 (5.15)

To deduce the kinetic energy, we need the velocity of the mass center C, which can be found as

VC = vP + e63 X b [(1 + a) – (1 + e)] bi (5.16)

where the inertial velocity of the reference point P is

v p = – hi2 (5.17)

and thus

vC = —hi2 + be (a – e)b2 (5.18)

The kinetic energy then is given by

11

K = 2mvc ■ vc + 2Ice2 (5.19)

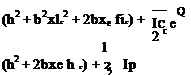where Ic is the moment of inertia about C. By virtue of the relationship between b2 and the inertially fixed unit vectors i1 and i2, assuming e to be small, we find that

where Ip = Ic + mb’2×2.

The generalized forces associated with the degrees of freedom h and e are de­rived easily from the work done by the aerodynamic lift through a virtual displace­ment of the point Q and by the aerodynamic pitching moment about Q through a virtual rotation of the model. The velocity of Q is

The virtual displacement of the point Q can be obtained simply by replacing the dot over each unknown in Eq. (5.21) with a S in front of it; that is

where 5pe is the virtual displacement at Q. The angular velocity of the wing is 0b3; therefore, the virtual rotation of the wing is simply 80b3. Hence, the virtual work of the aerodynamic forces is

and the generalized forces become

Qh = —L

(i (5.24)

Q0 = Mi + b ( 2 + aj L

It is clear that the generalized force associated with h is the negative of the lift, whereas the generalized force associated with 0 is the pitching moment about the reference point P.

Lagrange’s equations (see the Appendix, Eqs. A.35) are specialized here for the case in which the kinetic energy K depends on only qi, q2,…; therefore

Here, n = 2, qi = h, and q2 = 0 and the equations of motion become

m(h + bx00) + khh = — L

For the aerodynamics, the steady-flow theory used previously gives

L = 2npIX)bU20 Mi = 0

4

where, in accord with thin-airfoil theory, we have taken the lift-curve slope to be 2n. Assuming this representation to be adequate for now, we can apply the p method because the aerodynamic loads are specified for arbitrary motion. (We subsequently consider more sophisticated aerodynamic theories.)

To simplify the notation, we introduce the uncoupled, natural frequencies at zero airspeed, defined by

Substituting Eqs. (5.27) into Eqs. (5.26), using the definitions in Eqs. (5.28), and rearranging the equations of motion into matrix form, we obtain

0 0

(5.29)

Note that the first equation was multiplied through by b and the variable h was divided by b to make every term in both equations have the same units. Following the p method as outlined previously, we now make the substitutions h = h exp(vt) and в = в exp(vt), which yields

mb2v2 + mb2a>2h mb2v2 xe + 2nplXJb2U2

mb2v2xe Iprn2e + Ipv2 – 2(a + l,)np^b2U2

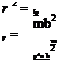Although this eigenvalue problem can be solved as it is written, it is more convenient to introduce dimensionless variables to further simplify the problem. To this end, we first let v = pU/b, where p is the unknown dimensionless, complex eigenvalue; divide all equations by mU2; and finally introduce the dimensionless parameters

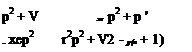Here, r is the dimensionless radius of gyration of the section about the reference point P with r2 > x2; a is the ratio of uncoupled plunge and pitch frequencies; p is the mass-ratio parameter reflecting the relative importance of the model mass to the mass of the air affected by the model; and V is the dimensionless freestream speed of the air, sometimes called the “reduced velocity.” As a result, the equations then simplify to

For a nontrivial solution to exist, the determinant of the coefficient matrix must be set equal to zero. There are typically two complex conjugate pairs of roots—for example

bv1 b,

pi = u = u (Гі ±1 ^x)

bv2 b,

p2 = U = U (Г2 ± 1 ^2)

A more convenient way to present these roots is to multiply them by the reduced velocity V, yielding

К, u r1 ^

— (Г1 ± і ^i) -— = — ± і —

U Ьшє Шв Шв

b,„ , – о л U Г2 . ,Й2

— (Г2 ± i &2)~ = ± i

U Ьшє шв шв

This way, they are now tied to a specified system parameter шв instead of the varying speed U.

For a given configuration and altitude, we must look at the behavior of the complex roots as functions of V and find the smallest value of V to give divergent

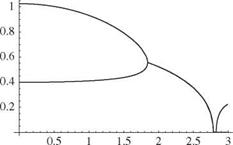
Figure 5.3. Plot of the modal frequency versus V for a = -1/5, e = -1/10, д = 20, r2 = 6/25, and a = 2/5 (steady-flow theory)

oscillations in accordance with Table 5.1. That value is VF = UF/{Ъшв), where UF is the flutter speed.

We may find the divergence speed by setting p = 0 in Eq. (5.32), which leads to setting the coefficient of в in the в equation equal to zero and solving the resulting expression for V. This value is the dimensionless divergence speed VD, given by

UD _ І д Ьюв Г 1 + 2a

This is the same answer that we would obtain with analyses similar to those presented in Chapter 4.

For looking at flutter, we consider a specific configuration defined by a = -1 /5, e = -1/10, д = 20, r2 = 6/25, and a = 2/5. The divergence speed for this configu­ration is VD = 2.828 (or UD = 2.828 bшв). Plots of the imaginary and real parts of the roots versus V are shown in Figs. 5.3 and 5.4, respectively. The negative of Г is the modal damping and ^ is the modal frequency. We consider first the imaginary parts, Й, as shown in Fig. 5.3. When V = 0, we expect the two dimensionless fre­quencies to be near unity and a for pitching and plunging oscillations, respectively. Even at V = 0, these modes are lightly coupled because of the nonzero off-diagonal terms proportional to xe in the mass matrix. As V increases, the frequencies start to

approach one another, and their respective mode shapes exhibit increasing coupling between plunge and pitch. Flutter occurs when the two modal frequencies coalesce, at which point the roots become complex conjugate pairs. At this condition, both modes are highly coupled pitch-plunge oscillations. The dimensionless flutter speed is VF = UF/(boje) = 1.843 and the flutter frequency is &F/шв = 0.5568. The real parts, Г, are shown in Fig. 5.4 and remain zero until flutter occurs. When flutter occurs, the real part of one of the roots is positive and the other is negative.

Comparing results from this analysis with experimental data, we find that a few elements of realism are at least qualitatively captured. For example, the analysis predicts that flutter occurs at a value of V = VF < VD, which is correct for the specified configuration. Furthermore, it shows a coalescence of the pitching and plunging frequencies as V approaches VF, which is not only correct for the specified configuration but also is frequently observed in connection with flutter analysis. However, the previous analysis is deficient in its ability to accurately predict flutter speed. Moreover, the damping of all modes below the flutter speed is predicted to be zero, which is known to be incorrect. Finally, the steady-flow theory exhibits a coalescence characterized by the two roots being exactly equal to one another at the point of flutter. This condition is not met at all in data obtained from experiments and flight testing.

These deficiencies in predictive capability stem from deficiencies in the aero­dynamic theory. The steady-flow aerodynamic theory of Chapter 4 was used. Al­though this aerodynamic theory has obvious deficiencies (e. g., linearity and two- dimensionality), a most significant deficiency concerning flutter analysis is that it neglects unsteady effects. To obtain an accurate prediction of flutter speed, it is necessary to include unsteadiness in the aerodynamic theory; this demands a more sophisticated aerodynamic theory.

Unfortunately, development of unsteady-aerodynamic theories is no small un­dertaking. Unsteady-aerodynamic theories can be developed most simply when sim­ple harmonic motion is assumed a priori. Although such limited theories cannot be used in the p method of flutter analysis described in Section 5.1, they can be used in classical flutter analysis, described in the next section. As will be shown, classi­cal flutter analysis can predict the flutter speed and flutter frequency, but it cannot predict values of modal damping and frequency away from the flutter condition. To obtain a reasonable sense of modal damping and frequencies at points other than the flutter condition, two approximate schemes are discussed in Section 5.4.

If these approximations turn out to be inadequate for predicting modal damping and frequencies, we have no choice but to carry out a flutter analysis that does not assume simple harmonic motion, which in turn requires a still more powerful aerodynamic theory. One such approach that fits easily into the framework of Sec­tion 5.1 is the finite-state theory of Peters et al. (1995). Such a theory not only facilitates the calculation of subcritical eigenvalues; because it is a time-domain model, it also can be used in control design.

Hence, in the following sections, we first look at classical flutter analysis and the approximate techniques associated therewith and then turn to a more detailed
discussion of unsteady aerodynamics, including one theory that assumes simple harmonic motion (i. e., the Theodorsen theory) and one that does not (i. e., the Peters finite-state theory).