Bayesian Update of the Uncertain Airfoil Geometry
We assume that the airfoil geometry contains random deformations (e. g. dents). A possible reason, for example, can be the influence of external forces. First our task is to parametrize all such deformations for all given airfoils. We offer to use random fields к(х, со), where со is a vector of random parameters (see Section 2.2). The problem is that the probability density function of о is unknown. We assume it a priori as Gaussian. If we could measure all given airfoils (from different airplains) then we could build a good parametrization model, but everything we can do is to measure airfoils only in a few points. This is our knowledge. The question now is how to incorporate this knowledge to our parametrization model? We can do this by using the Bayesian update. The Algorithm is described in [21, 20].
 |
 |
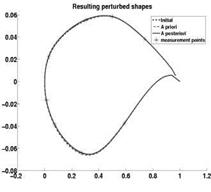
In Fig. 6 (left) you may see:
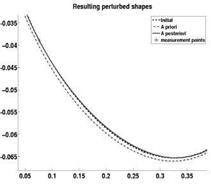
Fig. 6 (left) The truth airfoil (is in reality unknown), a priori (is our initial assumption) and a posteriori (the measurements are taken into account) airfoils. (right) Detailed RAE-2822 airfoil picture in interval [0.05, 0.35].
• The initial airfoil (dashed line). Is in real life, as a whole, unknown. One can measure it only in a few points.
• A priori realization (dash-dot line). One realization computed from the a priori model without any knowledge (without measurements). Usually does not coincide with the truth. Can be far away from the truth.
• A posteriori realization (solid line) is computed via the Bayesian update (see details of the Algorithm in [21, 20]) from the a posteriory model which takes into account the real data measured in the 8 measurement points (8 stars). Since large deformations are not allowed, all three curves are very similar. The detailed picture (in interval [0.05, 0.35]) is shown in Fig. 6 (right). One can see that the solid line (a posteriori model) is much closer to the measurement point (denoted by stars) than to the dash-dot line (a priori model).












