Rigid or Undistorted Wake
The rigid or undistorted vortex wake model is one in which the trailed vortices are represented by skewed helical filaments. The position of the vortex filaments is defined geometrically based on the flight conditions and momentum theory considerations. There are no self – or mutual-interactions, between vortex filaments. If we assume that the induced
velocity field in the wake is uniform (i. e., the induced velocity does not vary with time or location), then an exact analytical solution may be obtained for Eq. 10.53 as a special case. Making this assumption is equivalent to assuming a uniform streamwise velocity and a mean inflow, A; = constant throughout the flow, that is
![]() V = QRfii + QR(X[)k.
V = QRfii + QR(X[)k.
Under these assumptions, the PDE governing the wake geometry relative to the TPP (see Eq. 10.50) can be written as
 (10.69)
(10.69)
where іf/w is the wake age and fb is the azimuth angle of the blade at which the vortex filament was generated, also recognizing that the position vector r has now been nondimensionalized by R. Equation 10.69 is a linear, first-order, hyperbolic, PDE. The two required boundary conditions in the fb and directions are given by
![]() fb-r(fb, fw) = Hfb + 2л-, fw), fw’ r(fb, 0) = rv cos fbi + rv sin fbh
fb-r(fb, fw) = Hfb + 2л-, fw), fw’ r(fb, 0) = rv cos fbi + rv sin fbh
where rv is the radial release point of the trailed vortex filament from the blade (rv — 1 at the tip). The analytical solution to Eq. 10.69 can be obtained using separation of variables – see Hildebrand (1976). The solution of the PDE is defined by the characteristic curve of the equation, which can be determined from the intersection of the two surfaces found by integrating the following ODEs:
From Eqs. 10.72 and 10.73, the two surfaces are given by fb = fw + c and r = Vfw/ QR + C2, respectively, where c and c2 are constants of integration. From these solutions, ci — fb — fw and C2 = r — Vfw/Q. The intersection of the two surfaces results in an equation relating the two constants such that C2 = f{c) =» r — Vfw/QR = f(fb — fw)- Invoking the boundary condition at (rw — 0 results in r = rv cos xf/b і + rv sin xj/b j, and so the exact solution can be written as
r{fb, fw) = (ttfw + rv cos (fb – fw)) * + rv sin (ifrb – fw) ] + A ifw k. (10.74)
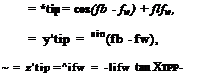 |
|
Notice that the periodic boundary condition in the yrb direction is also satisfied because cos(27r + j/b) = cos fb and sinfln + фь) = sin^- Equation 10.74 defines a skewed, undistorted helix, which is known as the rigid or undistorted vortex wake topology, which has already been introduced. If only tip vortices are assumed (rv = 1), then the solution for the tip-vortex geometry relative to the rotor TPP can be described by the simple parametric equations
where using the simple momentum theory in forward flight
and where к is an induced power factor. Notice that there is no contraction assumed in the rigid vortex wake. However, if it is found necessary to model this effect, the tip vortices can be assumed to originate at a point just inboard of the tip, say rv = 0.97. Also, note that with the rigid wake equations, as p 0 the wake geometry reduces to a helix, but as has been described previously, this is an unsatisfactory model of the wake in hover.
A rigid wake geometry is plotted in Fig. 10.33 for forward flight at д = 0.15 and is compared to predictions made by a FVM (see Section 10.7.6). Notice that the predictions are substantially different. Nevertheless, the simplicity of the rigid wake model will give the primary effects of the skewness of the wake on the inflow distribution over the rotor disk and may be attractive for applications where the full details of the rotor wake are not required, such as for integrated rotor performance predictions. (See also the results of the rotor wake boundary shown previously in Fig. 10.10).











