Role of the Reynolds Number

The Re number was introduced previously (see Chapter 2) as an important viscous-flow similarity parameter that strongly controls the viscous boundary-layer behavior. We now show how this similarity parameter appears as a major governing parameter in the incompressible viscous-flow equations. Steady, two-dimensional Cartesian flow is discussed for convenience, but all results are readily extended to time-dependent flows in three dimensions and to other coordinate systems. Because

The only parameter that appears in the resulting set of dimensionless equations:

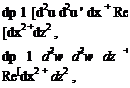du dw „

й+й=0

_ du _du u — + w—– dx dz

_dw _dw

u — + w — dx dz

is the coefficient (рУ^ L/p) = Re, the Reynolds number. The student should confirm that this also is true for the Navier-Stokes equations that describe three-dimensional flow. Additional dimensionless groups appear if the flow is unsteady or compress­ible. The Re number is a similarity parameter (see Chapter 2).

Suppose that a viscous-flow problem involving a body of given shape and size has a certain numerical value of the Re number and that the Navier-Stokes equations for this problem are written in dimensionless form and solved. Now, consider a second flow problem involving a body of geometrically similar shape (i. e., same shape and orientation to the flow but different size). If the Re number for this second case has the same magnitude as the first (even though the indi­vidual magnitudes of velocity, viscosity, and reference length are different in the two problems), then the solution to the first problem (in dimensionless form) is also the solution to the second problem. That is, any solution to Eq. 8.29 is also the solution for any other problem with geometrical similarity and the same Re number. This demonstrates one of many powerful features associated with the similarity concept.

We saw previously how exact solutions to the Navier-Stokes equations may be found for certain problems by using restrictive assumptions. The Navier-Stokes equations also may be simplified in two limiting cases distinguished by very small and by very large values of the Re number:

1. Flows with Re <<1.0. Such flows are called Stokes or Oseen flows. They correspond to very slow creeping fluid motion. The continuity and Navier-Stokes equations can be combined into a single linear equation, which is the starting point for the theory of lubrication and other important applications.

2. Flows with Re >> 1.0. This situation usually arises from a small coefficient of vis­cosity (as in most aerodynamics applications with atmospheric air as the medium) and leads to the Prandtl boundary-layer problem.

In the next section, we study this second case, which represents the important aerodynamics problem of viscous flow at high Re number over a surface such as an airplane wing. In such problems, the Re number is typically in the range of 106 to 107. Notice that the effects of viscosity in the dimensionless governing equation (Eq. 8.29) are represented by terms divided by this very large parameter. This suggests that the viscous effects are mathematically unimportant. In fact, it is this

feature that enabled us to solve external aerodynamics problems of the types intro­duced in preceding chapters without regard for the effect of viscous effects or fric­tional losses.

However, it is clear that viscous effects must be important near the surface of the body where the velocity must tend to zero. This paradox was resolved by the work of Prandtl in 1904. The answer is, of course, that one of the derivative terms multiplied by the inverse of the Re number must be very large so that the product is as important as other terms in the momentum balance. From the viewpoint of differential-equation theory, this gives rise to an important class of mathematical problems known as singular perturbation theory. The Prandtl boundary-layer problem was the first of this type to be solved; the central role of the Re number in its formulation and solution are the subject of the next section.