Steady, Incompressible Flow Between Two Semi-Infinite Parallel Plates

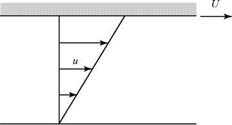
We consider two long parallel plates with a viscous fluid between them, as shown in Fig. 8.7. The fluid initially is at rest. At some time, the top plate is set in motion to the right with a constant velocity U. We are interested in the steady-flow problem—that is, after the plate has been in motion for a long time. This flow problem is called Couetteflow (see Schlichting, 2003).

With parallel flow again assumed, the defining equation is the same as Eq. 8.21. However, in the case of Couette flow, the problem is easier because no pressure difference is imposed on the flow between the two plates to make the fluid move. The fluid is moving as a consequence of the viscous force at the upper surface—it is being pulled along by the moving upper plate. Thus, there is no pressure dif­ference driving the flow, dp/dx = 0, and the defining equation for Couette flow reduces to:

d2u = d2u = о

a?=dX2 = ,

subject to the boundary conditions:

ulz = о = 0; ulz = H = u.

Integrating twice and evaluating the constants of integration using these boundary conditions, the result is a linear-velocity profile given by:

u = Hz, (8.24)

as shown in Fig. 8.7b. The student should verify this result. If a left-to-right – driving pressure difference is applied to the fluid between the two plates in Fig. 8.7, the solution to the resulting linear problem is a superposition of the

(a)

Figure 8.7. Couette flow.

linear-velocity profile of Couette flow and the parabolic profile found previously in Poiseuille flow.