Transition Models and Criteria

In the last two decades the knowledge of instability and transition phenom­ena has increased considerably, and many new and comprehensive stabil- ity/instability methods are now available. However, the accurate and reliable prediction of the shape, the extent and the location of the transition zone, i. e., the transition sub-branch IIb, Fig. 8.1, for real flight vehicles of the ve­hicle classes considered here is not possible.[147] This holds partly also for flows in the other speed regimes. Thus when we speak about transition prediction it is in the sense of transition estimation.

We distinguish three classes of means for transition prediction, namely

— non-empirical,

— semi-empirical,

— empirical

methods and criteria. Of these the latter two rely partly or fully on experi­mental data.

The major problem is that all-encompassing high-speed experimental data bases still are very scarce. These, in principle, could come either from ground – simulation facilities or from free-flight measurements. For the first it is noted that a hypersonic ground-simulation facility is not able to duplicate the at­mospheric flight environment and also not the relevant boundary-layer prop­erties, i. e., the profiles of the tangential velocity, the temperature and the density normal to the surface in presence of radiation cooling, as they are present on a real vehicle’s surface [7].

This holds especially for regular but also for forced transition. With regard to free-flight measurements we must observe that the available transition data sets obtained at actual high-speed flight, see, e. g., [106], are not always the necessary multi-parametric data bases, which are required to identify the major instability and transition phenomena involved, including the relevant flow and surface properties.

We give now a short overview over the three classes of methods and criteria for transition prediction, for the first two classes see also the review [101]. Regarding semi-empirical and empirical methods and criteria we note that it is necessary for a given practical application to make first a thorough assessment of the flow field under consideration as was done for instance in

Section 1.2. The data base underlying the method or criterion to be employed must correspond as accurately as possible to the considered flow field.

Non-empirical Transition Prediction. It appears that non-local non­linear instability methods have the real potential to become in the long term the needed non-empirical transition prediction methods for practical pur­poses. Direct numerical simulation (DNS) as well as large eddy simulation (LES), due to the needed very large computer power, will have, for a long time to come, their domain of application in numerical experiments of re­search only.

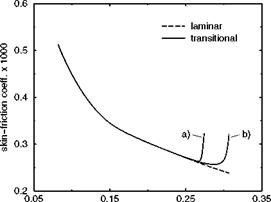
The present state of development of non-local non-linear methods ap­pears to permit the prediction of the location of stage 5, i. e., the beginning of sub-branch IIb, as for instance is demonstrated by Fig. 8.12 [43]. However, two different combinations of disturbance modes—a) and b)—lead to small, but significant differences between the solutions (location and initial shape of sub-branch IIb). This points to the problem of handling free-stream distur­bances, Sub-Section 8.3.2, which still is a major obstacle for the non-empirical transition prediction.

xc/c Fig. 8.12. Result of a non-local non-linear method [43]: rise of the skin-friction coefficient in stage 5, i. e., at the begin of sub-branch IIb. Swept wing, уLE = 21.75°, Ыж = 0.5, Rex = 27-106, two different disturbance mode combinations.

The result of Fig. 8.12 is for a low-speed case, similar results for the high­speed flows of interest are available to a certain extent. It can be expected, in view of the references given in Sub-Section 8.4.1, that at least results similar to those shown can be obtained, after additional research has been conducted, especially also with regard to the receptivity problem [101].

Very encouraging is in this context that the problem of surface irregulari­ties (transition triggering, permissible properties) seems to become amenable for non-empirical prediction methods, see [130], at least for transonic flow past swept wings.[148] That would allow to take into account the influence of weak surface irregularities on regular transition, but also to model transition forced, for example, by the rough tile surface of a TPS.

Semi-empirical Transition Prediction. Semi-empirical transition pre­diction methods go back to J. L. van Ingen [132], and A. M.O. Smith and N. Gamberoni [133]. They observed independently in the frame of local linear stability theory that, for a given boundary-layer mean flow, the envelope of the most amplified disturbances, see Fig. 8.7 for (two) examples, correlates observed transition locations.

For airfoils it turned out, that on average the value, see Sub-Section 8.1.2,

A t

In — = Midi = 9, (8.31)

A0 Jt о

best correlates the measured data, hence the name e9 criterion. Unfortunately later the “universal constant” 9 turned out to be a “universal variable”. Already in the data base of Smith and Gamberoni the scatter was up to 20 per cent. Now we speak of the en criterion, which for well defined flow classes with good experimental data bases can be a reliable and accurate transition prediction tool, see, e. g., [134]. The disturbance environment can be regarded to some degree. The free-stream turbulence Tu of a wind tunnel, for instance, can be taken into account by introducing ntr = ntr (Tu) [135]. Surface roughness can be treated, too.

The en method can be used by employing the parabolized stability equa­tions (PSE) approach [19]. The result is a linear, non-local method. With this method surface curvature and non-parallel effects can be taken into account.

For three-dimensional flows the situation becomes complicated, see, e. g., [107]. Non-local linear stability theory with n-factors for Tollmien-Schlichting modes (nTS) and for cross-flow modes (nCF), based on in-flight measured data, are used increasingly in transonic swept-wing flows, see the discussion in [28].

Although the en method does not describe at least the initial stage of tran­sition, i. e., the beginning of sub-branch IIb, it has been extensively applied to mainly two-dimensional high-speed flows [11, 134, 57]. It is a valuable tool to study instability phenomena and their influence on transition, but also to perform parametric studies. To reliably predict transition on hypersonic flight vehicles is primarily a matter of a reliable, all-encompassing multi-parametric experimental data base, which is not available. To question is also whether an en method permits to treat the effect of weak surface irregularities on regular transition, but also to describe forced transition. In [101] en methods
are seen as intermediate step along the way to non-empirical methods—there called mechanism-based methods—in hypersonic flows.

Empirical Transition Prediction. Empirical transition prediction is based on criteria derived from experimental data which are obtained in ground- simulation facilities but also in free flight. Such criteria have been applied and are applied in the design of the Space Shuttle Orbiter, of BURAN, of re-entry bodies, launchers, and missiles.

The empirical criteria usually are local criteria, i. e., they employ local integral boundary-layer and boundary-layer edge-flow properties. This means that all the phenomena discussed in Sub-Sections 8.1.3 to 8.2.9 are not taken into account explicitly. At best some of them are implicitly regarded via an employed boundary-layer integral quantity. Data from ground-simulation facilities are possibly falsified by tunnel noise effects. The lower (xtr, i) and the upper (xtr, u) transition location often are not explicitly given, i. e., length and shape of the transition sub-branch IIb, Fig. 8.1, are not specified. This holds also for the overshoot at the end of this branch.

Due to the nature of the criteria, the predictions based on them are of questionable quality. If error bars are given, uncertainties of describing data and hence design margins can be established. In any case parametric guesses can be made.

Empirical criteria are discussed in depth in, for instance, [11] and [57]. In [57] available high-speed flow criteria, in this case basically two-dimensional criteria, are grouped into four classes:

— Smooth body criteria, i. e., criteria to predict regular transition. A typical criterion from this class is the Thyson criterion [136]:

Res2,tr = 200 e0187 Me. (8.32)

Reg2 tr is the Reynolds number based on the boundary-layer edge data and the momentum thickness S2, Me is the edge Mach number. The correla­tion data are mainly from ground-simulation facilities and hence the noise problem exists.

To this class of criteria also the criterion by H. W. Kipp and R. V. Masek is counted [137]. Written in the general form

it can be applied to different configurations, although it was originally developed for the Space Shuttle Orbiter design. Stetson [11] discusses this criterion in detail and states that it cannot be applied in general.

— Rough body criteria, i. e., criteria to predict transition forced by single or distributed (TPS surface) roughnesses. As example a criterion for dis­tributed roughness, developed in the frame of the HERMES project with data from Space Shuttle Orbiter flights, is given [138, 57]:

The corrected roughness height kcorr is defined by

The roughness is efficient if located less than 6 m from the vehicle nose and k/S1 = 0.1 to 0.5.

The criterion takes into account the roughness height k, the boundary-layer edge data pe, ue, pe, the displacement thickness Ji, the boundary-layer edge Mach number Me, and the longitudinal curvature R. It is defined for the lower symmetry line of the vehicle and duplicates well the Space Shuttle Orbiter data there. The need for a truly three-dimensional approach is acknowledged by the authors.

— Combined rough/smooth body criteria, i. e., criteria with parameters to distinguish sub-critical and super-critical roughness regimes. An example is the criterion given by W. D. Goodrich et al. in order to improve the transition prediction for the Space Shuttle Orbiter [2].

— Global criteria take into account implicitly all phenomena of interest for a given vehicle class. In [139], for instance, data are correlated for ballistic re-entry vehicles with ablative nose tips, however with mixed success.

More recent publications regarding ground facility and flight data can be found in [42, 106] and [140]-[142].

Criteria, which take into account effects of three-dimensionality, for in­stance, cross-flow instability or attachment-line contamination are discussed too in [57]. We have treated them in Section 8.2.