Dynamic Inflow
The forgoing description of a physical behavior forms a fundamental basis for the development of nonsteady (and perhaps aperiodic) wake models. Carpenter & Friedovich (1953) attributed the buildup of the mean rotor inflow and rotor thrust to inertia effects in the flow. To model this behavior, a dynamic inflow equation was formulated by equating the rotor thrust obtained using differential momentum theory to that using blade-element theory (i. e., the BEMT discussed in Chapter 3). Unsteady inflow effects were modeled using the concept of an apparent mass (inertia), where the thrust equation (as given by the momentum theory in Chapter 2) is modified by the addition of an unsteady term to give
![]() (10.108)
(10.108)
The term ma was associated by Carpenter & Friedovich (1953) with the apparent mass of an impermeable (solid) circular disk accelerating in a stagnant fluid, that is, a noncirculatory effect. It was further suggested that this apparent mass to be 63.7% the mass of a sphere of fluid with a radius equal to the rotor radius, that is,
![]()
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|
||
|
|||
|
|||
|
|||
|
|||
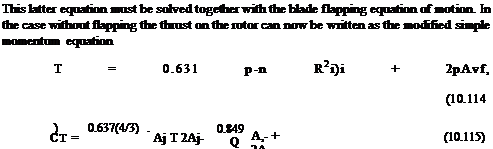 |
|||
|
|||
|
|||
|
|||
|
|||
![]()
![]()
For a typical helicopter rotor where X,- ~ 0.05 and Q ъ 40 rad/s, will be of the order of 0.1 seconds. The dynamic adjustments that take place in the time averaged inflow are, therefore, relatively rapid in real time. However, it will be noted that a time lag of 0.1 seconds corresponds to over half a rotor revolution, so at the local (blade element) level the local adjustments to the flow do, in fact, occur over relatively long aerodynamic time scales in terms of wake age or semi-chords of blade travel.











