Flow Past a Circular Cylinder with Circulation

We saw that there is no net force acting on a circular cylinder in a steady irrotational flow without circulation. It can be shown that a lateral force identical to a lift force on an aerofoil, results when circulation is introduced around the cylinder. When a clockwise line vortex of circulation Г is superposed around the cylinder in an irrotational flow, the stream function [sum of Equations (2.43) and (2.48)]

becomes:

The tangential velocity component at any point in the flow is:

At the surface of the cylinder of radius a, the tangential velocity becomes:

Ve I _ = -2 Vx sin в – —. 1 r=a 2n a

At the stagnation point, Ve = 0, thus:

For Г = 0, the potential flow past the cylinder is symmetrical about both x – and y-directions, as shown in Figure 2.19(a). For this case there is no drag acting on the cylinder.

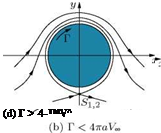
For Г < 4 n a Vx, two values of в satisfy Equation (2.52). This implies that there are two stagnation points on the surface, as shown in Figure 2.19(b).

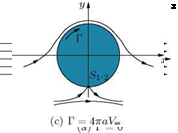
When Г = 4 n a Vx, the stagnation points merge on the negative y-axis, as shown in Figure 2.19(c). For Г > 4 ж a Vx the stagnation points merge and stay outside the cylinder, as shown in Figure 2.19(d). The stagnation points move away from the cylinder surface, since sin в cannot be greater than 1. The

radial distance of the stagnation points for this case can be found from:

This gives:

Г ± V7Г2 – (4na Vm)2

One root of this is r > a, and the flow field for this is as shown in Figure 2.19(d), with the stagnation points S and S2, overlapping and positioned outside the cylinder. The second root corresponds to a stagnation point inside the cylinder. But the stagnation point for flow past a cylinder cannot be inside the cylinder. Therefore, the second solution is an impossible one.

As shown in Figure 2.19, the location of the forward and rear stagnation points on the cylinder can be adjusted by controlling the magnitude of the circulation Г. The circulation which positions the stagnation points in proximity, as shown in Figure 2.19(b), is called subcritical circulation, the circulation which makes the stagnation points coincide at the surface of the cylinder, as shown in Figure 2.19(c), is called critical circulation, and the circulation which makes the stagnation points coincide and take a position outside the surface of the cylinder, as shown in Figure 2.19(d), is called supercritical circulation.

To determine the magnitude of the transverse force acting on the cylinder, it is essential to find the pressure distribution around the cylinder. Since the flow is irrotational, Bernoulli’s equation can be applied between a point in the freestream flow and a point on the surface of the cylinder. Bernoulli’s equation for incompressible flow is:

Using Equation (2.52), the surface pressure can be found as follows.

At the surface r — a and Equation (2.51) gives the local velocity at any point on the surface as:

V0| _ — -2 Vm sin в – Г

‘r—a 2n a

Substituting this into Bernoulli’s equation, we get:

that is:

The symmetry of flow about the y-axis implies that the pressure force on the cylinder has no component along the x-axis. The pressure force acting in the direction normal to the flow (along y-axis) is called the lift force L in aerodynamics.

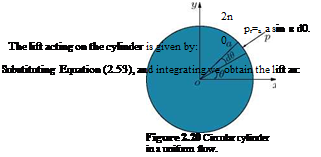
Consider a cylinder of radius a in a uniform flow of velocity Vm, shown in Figure 2.20.

where we have used:

2n 2n

sin ede = sin3 в de = 0.

00

It can be shown that Equation (2.54) is valid for irrotational flows around any two-dimensional shape, not Just for circular cylinders alone. The expression for lift in Equation (2.54) shows that the lift force proportional to circulation Г is of fundamental importance in aerodynamics. Wilhelm Kutta (1902), the German mathematician, and Nikolai Zhukovsky (1906), the Russian aerodynamicist, have proved the relation for lift, given by Equation (2.54), independently; this is called the Kutta-Zhukovskylift theorem (the name Zhukovsky is transliterated as Joukowsky in older Western texts). The circulation developed by certain two-dimensional shapes, such as aerofoil, when placed in a stream can be explained with vortex theory. It can be shown that the viscosity of the fluid is responsible for the development of circulation. The magnitude of circulation, however, is independent of viscosity, and depends on the flow speed Vx, the shape and orientation of the body to the freestream direction.

For a circular cylinder in a potential flow, the only way to develop circulation is by rotating it in a flow stream. Although viscous effects are important in this case, the observed pattern for high rotational speeds displays a striking similarity to the ideal flow pattern for Г > 4naVx,. When the cylinder rotates at low speeds, the retarded flow in the boundary layer is not able to overcome the adverse pressure gradient over the rear surface (downstream of в = 90°) the cylinder. This leads to the separation of the real (actual) flow, unlike the irrotational flow which does not separate. However, even in the presence of separation, observed speeds are higher on the upper surface of the cylinder, implying the existence of a lift force.

A second reason for a rotating cylinder generating lift is the asymmetry to the flow pattern, caused by the delayed separation on the upper surface of the cylinder. The asymmetry results in the generation of the lift force. The contribution of this mechanism is small for two-dimensional objects such as circular cylinder, but it is the only mechanism for the side force experienced by spinning three-dimensional
objects such as soccer, tennis and golf balls. The lateral force experienced by rotating bodies is called the Magnus effect. The horizontal component of the force on the cylinder, due to the pressure, in general is called drag. For the cylinder, shown in Figure 2.20, the drag is given by: /»2п

I pr=a a cos в dd.

0

It is interesting to note that the drag is equal to zero. It is important to realize that this result is obtained on the assumption that the flow is inviscid. In real (actual or viscous) flows the cylinder will experience a finite drag force acting on it due to viscous friction and flow separation.