Lifting Line Theory (3-D Inviscid Flow)

15.2.2.1 Flow Model

The vortex sheet is a stream surface, wetted on both sides by the fluid, hence the tangency condition imposes that the ш-component of the perturbation be continuous. Across the vortex sheet the pressure is continuous, hence the u-component of the perturbation is continuous (Cp = —2u/U).

Velocity vectors near the vortex sheet: see Fig. 15.4.

Fig. 15.4 Induced velocities near the vortex sheet

15.2.2.2 Improved Lift of a Rectangular Wing

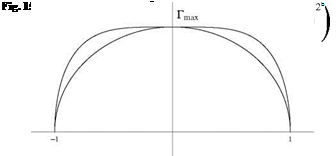
The combination of modes 1 and 3 is represented in Fig. 15.5.

The total lift of a wing is given solely in terms of A1 and can be written as CL = n AR A1. The maximum circulation is obtained for t = | and is rmax = 16 UbA1. Hence A1 = 1тиъ and the corresponding lift is Cl = n AR jU = 8 (cl )eUiptic, a

12.5 % increase for the high lift rectangular wing.

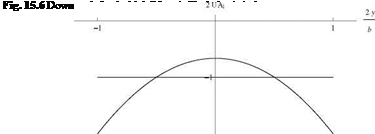
As seen in class, the downwash for the high lift wing is given by

The distribution of downwash is parabolic and is compared with that of the elliptic wing WT[y(t^elliptic = –Ir. See Fig. 15.6.

15.2.2.3 Drag Penalty

The induced drag of the wing is given by

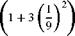
CDi = nAR a2^1 + ‘"+nAl + ••• ^ = nAR a2 The drag penalty is a 3.7 % increase in induced drag.