The design of warped wings with attached flow
6.6 To maintain the same type of flow throughout the flight range and, specifically, to obtain a flow with separation all along the leading edges and coiled vortex sheets on one side of the wing only, the wings must have such a shape that attachment lines lie all along the leading edges at one particular condition. All wings with flat chordal planes fulfil this condition automatically, at Cl = 0 . If this condition is to be fulfilled at Cl Ф 0 , the wing must be cambered and twisted or warped, in such a way that the load falls to zero along the edges at this design point. For CL > 0 , the leading edges are then bent down into the local flow direction, and the appropriate behaviour of the load is to vanish like the square root of the distance from the edge. The practical purpose of designing warped wings for attachment at Cl > 0 may be to reduce the lift – dependent drag or to trim the aircraft. Here, we discuss how such wings can be designed for low speeds, leaving the design of warped wings for supersonic speeds to section 6.8.
We note that the existence of such attachment design points constitutes only a necessary condition to obtain the desired type of flow – they are not likely
to be actual operating points of an aircraft. An aircraft is likely to fly, at any speed, at a lift coefficient above the attachment Cl, when the flow is separated from the edges. A complete design method should, therefore, be able to deal with both attached and separated flows but, as we have seen in section 6.4, existing design methods for separated flows are poor. Thus a complete design method is not yet established, and this makes it somewhat uncertain what precisely the design aims for the attached-flow condition should be. On the other hand, several theoretical approaches are available to design wings for attached flow, which lead to satisfactory results because, in general, we have a flow with genuinely small disturbances. The approximate equations of motions to be used are, of course, the same as those which have been used in the design of swept wings (see Chapter 5), but the solutions are not now in a form which allows special physical effects, such as kink effects on swept wings, to be identified. This makes it more difficult to formulate physically reasonable and effective design aims.
These matters have some repercussions especially on the design of wings to have low vortex drag. We have already noted that we are not able to calculate the wing shapes which give the smallest vortex drag for a given lift and span, when the downwash along the non-planar vortex sheet, shed from a slender wing with leading-edge separations, should be constant. If, on the other hand, the trailing vortex sheet could be assumed to be essentially planar, then the lower bound of the vortex drag factor in frictionless flow is known to be Kv = 1 , according to R T Jones (1951). But this requires the spanwise distribution of the chord loading to be elliptic, with an infinite slope at the tips, which is, in general, incompatible with our condition that, even in attached flow, the load should be zero along the leading edges, when the span – wise distribution of chord load has zero slope at the tips (as in Fig. 6.37). Thus we do not know how low the vortex drag can be, and we can set ourselves only the rather vague design aim to find wings with ‘a low drag’.
We are dealing here with threedimensional subsonic potential flows which are governed by (2.2). For the present purpose, this may be simplified and the boundary conditions may be applied in various ways, so that there are four main approaches and approximations, which are summarised in the table below and labelled (1) to (4). We are already familiar with these approximations:
|
Differential equation: |
ф + ф =0 yy zz |
(l – М^ф + ф + ф =0 0/Yxx yy Tzz |
|
Boundary condition: |
(о |
(2) |
|
in a mean plane |
slender thin-wing theory |
subsonic linear theory |
|
(3) |
(4) |
|
|
on the wing surface |
slender-body theory |
surface panel methods |
if the perturbations can be assumed to be small, (2.2) can be simplified into
(2.28) with 6^ = 1 “ м2 , the differential equation for cases (2) and (4) in
the table above. If, in addition, the wing can be assumed to be slender, or if the Mach number can be assumed to be near unity, then (2.28) can be simplified into (3.17), the differential equation for cases (1) and (3) in the table above. A further distinction can be made as to where the boundary conditions are to be applied: either in a mean chordal plane, cases (1) and (2); or on the wing surface, cases (3) and (4). Calculation methods have been developed for all four cases.
The earliest method for slender wings, case (1)» is that by R T Jones (1946) (see also J R Spreiter (1948) and G N Ward (1949) for a discussion of the assumptions and errors involved in this method). The downwash vz(x, y)/VQ induced by a specified load £(x, y) over the wing surface is then given by
(4.66) . R T Jones’s solution for a flat thin wing has already been quoted in
(4.67) to (4.69). There are also several theories which may be regarded as being halfway between the cases listed in the table. We refer to those for not-so-thin wings by J C Cooke (1962) and for not-so-8tender-wingв by
Mac C Adams & W R Sears (1953) and by L C Squire (1960). J H В Smith (1958),
J C Cooke (1960), D Hummel (1968), and H Portnoy (1968) have applied slender – body theory, case (3); and a surface-panel method, case (4), which is adapted for slender wings, has been developed by A Roberts & К Rundle (1972). However, most of these methods do not deal directly with the design problem which we want to discuss here. Also, we have already seen (see Fig. 6.11) that some of the theories are based on a physically unrealistic model of the flow, which allows infinite velocities around the edges.
There are several practical methods for the design of warped wings according to slender thin-wing theory, case (1), notably those by G G Brebner (1957) and (1958) and by J H В Smith & К W Mangier (1957), all these for delta wings with conical camber; and by J Weber (1957) and (1960) for more general slender shapes. In all cases, the load £(x, y) and the downwash vz(x, y) are related by (4.66), and the downwash is related by the boundary condition to the slope of the chordal mean surface, from which the shape of this surface can be obtained by integration. The assumptions of this theory allow thickness effects to be treated separately from lift effects, so that a chosen thickness distribution can be added to the ordinates z(x, y) of the mean surface. In principle, the load can be prescribed and the shape determined, but it is not obvious what load distribution should be chosen. If the load is expressed as a sum of basic solutions, to allow some choice, then the resulting wing shape, as well as the pressure distribution, may exhibit undesirable waviness. This is avoided in a method by R К Вега (1974) for warping delta wings to give minimum vortex drag.
J Weber (1957) and (1960) avoids waviness by applying a mixed procedure: partly, the wing shape is prescribed and, partly, some property of the toad distribution. For example, the inner part of the wing may be chosen to be flat inboard of shoulder tines, while the load falls to zero at the edges over the drooped outer parts of the wing. This is illustrated in Fig. 6.57. Aditionally, it may be specified that a hinge-tine suitable for trailing-edge controls should be straight in an otherwise warped wing. Alternatively, dihedral and anhedral may be incorporated, as discussed in relation to Fig. 6.55. Weber’s method is general enough to deal with wings with pointed nose and unswept trailing edge but otherwise arbitrary planform, with curved stream – wise and spanwise sections. A variety of aerodynamic conditions can be satisfied, though not necessarily all at once: the pressure distribution may be chosen; in particular, adverse pressure gradients may be limited; the position of the centre of load may be specified; the drag due to lift may be reduced below that of the corresponding plane wing. One can also choose from a variety of shapes to find one that meets non-aerodynamic requirements, such as a restriction on undercarriage length. However, it is never quite clear what the choice should be and how the wing will behave in off-design conditions.
P В Earnshaw (1963) has tested an extensive series of warped wings, designed by Weber’s method and covering a wide range of parameters. The main result of these tests was an indication that the attachment condition could indeed be
|
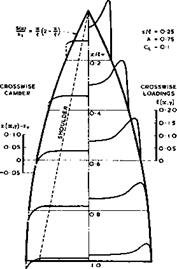
Fig. 6.57 A warped gothic wing. After J Weber (1957) |
fulfilled near the design lift coefficient, and that the flow development was regular in off-design conditions. The results also indicated the shortcoming to be expected from any slender-wing theory: trailing-edge effects, which are not taken into account in such a theory, dominate the difference between the load distributions achieved in the tests and those predicted by slender-wing theory. The agreement with design values of lift and pitching moment was good only when an appreciable part of the design load was carried over the forward part of the wing.
This particular shortcoming can be overcome by the application of subsonic linear theory, case (2), or surface-panel methods, case (4). Both involve much more numerical work, but this can be carried out by a computer. In linear theory, the design probelm to determine the shape of the mean surface to sustain a given loading £(x, y) involves the evaluation of the general downwash integral (4.49). This has been expressed in a form suitable for direct numerical evaluation by M P Carr (1968), following a procedure originally devised by J H В Smith et al. (1965) to solve the corresponding problem for supersonic flows (see section 6.8). An account of the method has been given by P J Davies (1971). This method corresponds to that of С C L Sells
(1969) for swept wings (see section 4.3), except that Sells’s method is more general in that it allows the downwash to be evaluated at any point on or off the mean surface.
In practical applications, one would like, in principle, to be able to specify the pressure distribution over the surface of a thick warped wing, as in the design of swept wings. Such designs have not yet been carried out. Instead, a given volume distribution Zy(x, y) is usually added to the mean surface and the pressure distribution due to volume determined separately. and added to the pressures due to lift, within the assumptions of linearised theory. The wing thickness Zy(x, y) is usually added to the mean surface in a constant direction normal to the plane of the planform, but P J Davies (1971) has shown
that, to preserve the attachment condition of the warp surface, it is more appropriate to add zv(x, y) at each point in the direction normal to the mean surface.
For completeness, we write down here how the pressure distribution due to thickness may be determined according to the linearised theory of subsonic flow past thin wings, case (2). As explained before (see section 4.3), the volume distribution is represented by a distribution of sources over the plan – form, where the source strength is twice the streamwise slope of the ordinate of the upper surface of a symmetrical wing. The disturbance velocity potential of this flow is
![]()
![]()
![]()
![]() ___________ dx’dy’__________
___________ dx’dy’__________
[(x – x’)2 + e2(y – y’)2 + e2z2]* ’
…. (6.45)
With the linearised approximation for the pressure coefficient
![]() г _ _ _!i±
г _ _ _!i±
P " VQ Эх ‘
the pressure coefficient at a point (x, y) on the wing is
This can be integrated by parts with respect to x’ , and P J Davies (1971), following M P Carr (1968), has shown how the differentiation with respect to x can then lead to an expression for Cp which is easy to evaluate numerically for sharp-edged wings, on which the slope is finite everywhere:
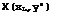 4ST
4ST
![]() Jg 1 [(X – X)2 + e2(y – y’)2]*
Jg 1 [(X – X)2 + e2(y – y’)2]*
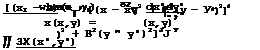 |
|
L ST L
and x^(y) and x^(y) are the values of x at the leading and trailing edges. The integration has been programmed by M P Carr (1968). We note that this procedure is more straightforward than the corresponding treatment of
swept wings with round leading edges and with strong centre and tip effects. Although this theory predicts an unrealistic logarithmic singularity along the leading and trailing edges, the regions affected by the singularity are small.
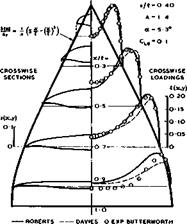
Davies’s method has been used to design several thick wings with various given loadings for testing in a low-speed windtunnel (see P J Butterworth (1970)). These wings are thought to be suitable for a subsonic allwing aerobus like that to be discussed in Chapter 7. For this application, s/l can be larger than for wings to fly at supersonic speeds. Also, the wing is thick enough (t/c = 0.09 at the centre line) to house the passenger cabin of an aircraft of medium size. An example is reproduced in Fig. 6.58 from an assessment of
|
Fig. 6.58 A warped mild-gothic wing. After P J Davies (1974) |
the accuracy of the design method by P J Davies (1973). This wing was designed to have a lift coefficient of = 0.1 and a centre of pressure
at the position хСр/Л = 0.533 at the attachment angle of incidence of ad = 5.3°. The results in Fig. 6.58 include not only the design calculations but also some obtained by the panel method of A Roberts & К Rundle (1972).
The latter is a direct calculation, producing the properties of a given shape, rather than a design calculation. It should be more accurate than linearised thin-wing theory because it takes proper account of the interference between the finite thickness and the warp of the wing, except near the leading edges where the required behaviour is not correctly represented. The comparison in Fig. 6.58 shows some differences between the loading distributions calculated from the two theories. Also, the overall lift from Roberts’s non-linear theory is nearly 10% higher than that from linear theory, and the centre of pressure is about 2% of the overall length further back at xCp/£ = 0.556 , in this particular case. No consistent improvement of the results from linearised theory could be obtained by adding second-order terms obtained from Bernoulli’s equation to the right-hand side of (6.46). Such an improvement requires the inclusion of second-order terms introduced through the boundary conditions, as in the general method by J Weber (1972).
Comparison with the experimental results by P J Butterworth (1970) in Fig.
6.58 for the design angle of incidence indicates that Roberts’s theory gives,
on the whole, a slightly better representation. But both theories are seen to be inadequate near the trailing edge where the actual load is significantly lower, presumably because of the displacement effect of the boundary layer. Consequently, the measured overall lift is also lower and happens to be close to that predicted by linear theory. The loss of lift at the rear also causes the experimental position of the centre of pressure to be ahead of both theoretical predictions. Thus the effects of viscosity should be taken into account in a complete design method. This could be done, in principle, in a way similar to that explained for swept wings in section 4.5, but such calculations have not yet been carried out.
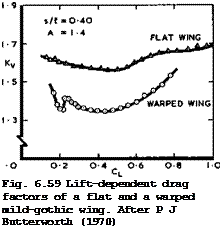
The experiment confirmed that attached flow was obtained at the design angle of incidence also in this example, and that separated flow developed in a regular manner at all other angles of incidence. Further, the lift-dependent drag was substantially reduced by the application of warp, as can be seen from the experimental results in Fig. 6.59. It is interesting to note that the
 LIVE GRAPH
LIVE GRAPH
Click here to view drag reduction is spread over the whole C^-range tested and that it is greatest at CL-values well above the design value “ 0.1 for attached flow: the leading-edge vortex sheets induce suction forces over forward-facing surfaces. This emphasises again the need for a complete design method for warped slender wings, which can take flow separation into account. Only then can an attempt be made to obtain much more substantial drag reductions than those achieved so far. It may be significant in this context to point out that all the loadings we have seen in Figs. 6.11, 6.26, 6.27, 6.43, 6.57 and 6.58, whether for attached or for separated flow, have in common that the middle part of the wing is only lightly loaded and that the main loading is always concentrated near the leading edges. As explained in section 6.4, this can have undesirable repercussions on the vortex drag. Sweptback wings also tend to have a lift deficiency in the middle but we know how to eliminate this by suitable design, at least for subcritical flow; with slender wings, we have not yet succeeded.
An interesting application of the slender-wing concept is the fleanhle wing or paraglider. In its simplest form, this may be a wing of delta planform, consisting of a sail-like flexible surface stretched between rigid beams along the leading edges. Other shapes may have two lobes between the leading edges and a third rigid beam along the middle. Any load is usually suspended below
the wing. Paragliders were first proposed by F M Rogallo & I 6 Lowry (1960) to transport space vehicles back to the ground after re-entry into the atmosphere. More recently, they have been used as actual gliders. These highly cambered wings provide an instructive example of the application of slender – body theory (see e. g. J N Nielsen (1965)), together with the aerodynamic theory of sails (see e. g. В Thwaites (1961)). A great deal of theoretical and experimental work has been done, and this has been summarised and extended by К Gersten & W H Hucho (1965). Gersten calculated the shape and the pressure distribution of one-lobed wings in attached potential flow, making the assumptions that the wings are slender and that the flow is conical. The material of the wing is assumed to be flexible but impermeable and inextensible. Under load, tension is assumed to act only in the spanwise direction. This tension T is then related to the pressure difference Ap and the radius of curvature R at any point by Ap/T = -1/R. Gersten obtained two approximations in. closed form, one for small camber and another for large camber, for an assumed family of contours. Experiments at low speeds showed that the wing shape is fairly well represented by this theory. But calculated and measured pressure distributions showed significant differences, especially at high angles of incidence. These were attributed by Gersten to the fact that the flow separated from the leading edges, after all.