The z-Velocity Component in the Boundary Layer

Notice that although we have not required anything from the z–component of the momentum equation other than information regarding the pressure gradient normal to the surface, it does not mean that there is no velocity component in the z-direction. This is a misunderstood feature of boundary-layer theory. Because there is a momentum deficit near the surface (i. e., the flow speed in the parallel direction must decrease to zero to satisfy the no-slip requirement), the result is a velocity com­ponent normal to the surface. That it is required by continuity is seen easily because from the first of Eq. (8.37):

which shows that the normal velocity is zero at the surface (as is required by the solid-wall-boundary condition) and increases to a maximum as the edge of the boundary layer is approached. This result also shows that the normal velocity is very small because it is proportional to the square root of the product of the freestream velocity and the viscosity coefficient.

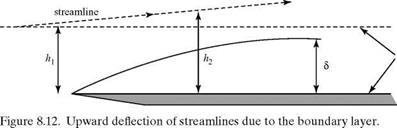
Figure 8.12 shows the behavior of the flow near the leading edge of the plate and indicates the upward deflection of the streamlines resulting from the formation of the boundary layer.

The magnitude of the z-velocity decreases as distance along the plate increases; that is, the first term in Eq. 8.54 decreases as the inverse of the square root of x whereas the second term decreases faster because it is inversely dependent on x. Far down­stream, there is no normal velocity. Equation 8.54 also demonstrates a fault with the theoretical results. Notice that at the leading edge of the plate, the simple theory pre­dicts that the normal velocity must be infinite because x = 0 at that point. This is a result of failure of our assumptions regarding relative sizes of the various quantities in proximity to the leading edge. That is, the simplified equations do not hold there. This defect can be corrected by application of powerful singular-perturbation methods that are based on the simple analysis we used. It is beyond the scope of this book to discuss these so-called leading-edge corrections. It also is possible to resort to a com­plete two-dimensional, CFD numerical solution in which derivatives in both the x – and z-directions are represented with finite difference formulas. If care is taken to use a suf – ficently fine grid near the leading edge, the apparent mathematical difficulty (usually referred to as a singularity) can be resolved. The CFD solution method is introduced in the next subsection. However, it displays the same defect at the leading edge that we just discovered because it attempts to solve the simple Blasius equation rather than the complete two-dimensional, Navier-Stokes equations. In other words, the defect is in the simplified differential equation rather than in the method of solution.