Performance considerations
To obtain a first rough survey of the possible performance of this type of aircraft and of the main propulsion and structural aspects, we shall adapt the simple first-order performance analysis of section 4.1 for the present purpose and change some of the assumptions to make them more suitable for short-range aircraft. But it should be clear from the outset that some of the concepts used before, such as the Brdguet range, tend to become inadequate for flight over short ranges (see e. g. D H Peckham
(1974) ). We illustrate this by quoting first some results from an analytical treatment of the performance of short-range aircraft by S В Gates (1965), which brings out clearly those parameters that really matter and can provide a sense of direction to other numerical work. In this analysis, the basic assumptions are: the flight path consists of a climb, followed by cruise at constant speed and height, followed by a descent, and it is always below the tropopause; the slope of the path is small so that its square, and thus the curvature of the path, may be neglected; as a first approximation, the weight is constant, and so the lift is equal to the weight throughout; the fuel used, though neglected as a fraction of the weight, is itself a vital part of the economy of the short-range service; and finally, the Mach number never exceeds the critical value, and so the drag coefficient remains essentially constant.
The motion of the aircraft is then governed by (6.7) which can be written as
an equation for the flight path
![]()
where t is the time. The engine thrust Th can be put equal to the sea – level thrust times a function of the density p(h) and the flight speed V. The lift-to-drag ratio is a function of Cl. The distance travelled and the time this takes can then be worked out, as well as the fuel used, if the specific fuel consumption of the engine is known.
The main conclusions from Gates’ analysis for flights over ranges of about 400km and of about 30 to 50 minutes duration are as follows:
(1) It seems probable that the installed thrust will be fixed by the airfield ;performance. The latter is also important with regard to the time spent on the airfield, which may be as much as one-third of the total time of flight.
(2) Once the aircraft has taken off, two broad alternatives for the flight ■path are open:
(a) Level acceleration near the ground to some high speed, which is then held constant for the rest of the flight. The flight time is constant on all such paths, and height can be used to economise fuel.
(b) Level acceleration near the ground to some speed less than the constant speed of case (a), followed by the rest of the flight at a speed which increases with height. A simple and practical example of this alternative is flight at constant JpV^ or constant equivalent airspeed. In all such paths, the time is a minimum when the whole flight is spent on climb and descent, and it is likely that this condition minimises the fuel as well. Typical examples of this kind are illustrated in Fig. 7.3.
Work of this nature is by no means complete and further studies should lead to firmer conclusions. In particular, existing methods for estimating in more detail take-off and landing manoeuvres could be applied (see e. g. D H Perry
(1969) and (1970) and R F A Keating (1974)), as well as multivariate analysis (see e. g. D L I Kirkpatrick & Joan Collingbourne (1973) and D L I Kirkpatrick (1974)) to obtain refined numerical answers under realistic constraints. But the general trends are reasonably clear and have been supported by the studies of G H Lee (1965). We note, in particular, that it pays to fly fast (at Mo = 0.8, say) and to fly high (at h = 6km, say), even over short ranges.
We can now consider some aspects of the engineering feasibility of the slender allwing concept and carry out a performance analysis and weight breakdown like that described in sections 4.1 and 6.2 but adapt it to the present purpose.
The various weight items, which add up to the given all-up weight, are now:
|
wuc |
= 0.05W |
undercarriage |
|
w S |
= 0.05W |
services and equipment |
|
w p |
payload |
|
|
WFU |
= 0.5W p |
furnishings etc. |
|
WF |
fuel used |
|
WR = 0.1W |
reserve fuel |
|
WE |
installed engine |
|
ww |
wing, including cabin |
 |
This list is largely the same as that for the supersonic slender aircraft in section 6.2, except that the weight of the furnishings has been reduced to indicate that less comfort might be provided in a short-range aerobus service
by (4.3). This assumes that the range R is given by BrAguet’s relation (1.7), which cannot be correct for flight paths like those in Fig. 7.3, but the error introduced by this in the weight analysis is not large, because the fuel fraction will generally turn out to be small. In the numerical examples below, we put R – 600km, i. e. between the values mentioned above. The
propulsive efficiency in subsonic flight is taken to be well below that at supersonic speeds, at rip = 0.25 . Other numerical values are Cdf = 0.0065 for the zero-lift drag coefficient, which is the same as that used in section 6.2; and A/K = 1 , which may be interpreted as implying a value of A near
1.5, or s/A near 0.35, and К = 1.5 . The maximum value of L/D is then about 11, which is consistent with the curve shown in Fig. 7.1.
The main change, the effect of which we want to demonstrate, is that the thrust and weight of the engine are to be determined from airfield rather than oruise considerations. Thus (6.5) is not now used. On the airfield, (6.6) and (6.8) still apply, and we note here that the factor 0.3 in (6.6) may be rather high and could possibly be lower for turbofan engines of high bypass ratio. It remains to find a relation for the thrust-to-weight ratio Tha/W for a prescribed field length. One that is suitable for our purpose has been derived by G H Lee (1965);
(see also D KUchemann & J Weber (1966)). Here, 6a is the climb angle and X is a parameter proportional to the field length; a typical value of X – lOkN/m^ corresponds to a relatively short runway of about 1400m length up to lift-off. A remarkable feature of this relation is that Tha/W depends only on the square root of the term (W/S)/(A/K) .
The various weight items can now be put together and the payload fraction determined:
We note first of all that, in contrast to the corresponding equation (4.10) for the classical aircraft, the parameter n appears in (7.5) only in the last term (fuel used). Hence, the question of finding an optimum value of n is now trivial: the largest payload fraction is obtained when n = 1 or nearly 1 (depending on how К varies with C^), i. e. when the aircraft flies near a CL~value which corresponds to the maximum of L/D, as assumed in Fig. 7.1.
We note further that the aspect ratio appears in such a way that the payload increases with increasing A/K. But the wing loading W/S now appears in two terms which oppose each other. They arise from the wing weight, which decreases with increasing wing loading, and from the engine weight, which increases.
There are several ways to determine the value of the wing loading which gives the highest payload fraction. If (7.5) is used directly without further constraints, assuming n = 1 , an optimum value of W/S can be calculated and
turns out to be
For the set of numerical values used above, the optimum values of W/S lie between 1 and 2kN/m^ and the corresponding payload fraction is about 0.3. But flying at the Ci/-value where L/D has its maximum, which this optimisation procedure implies, may lead to excessive cruising heights, even above the tropopause. This would not be consistent with very short ranges and might require engines with more thrust and weight than were needed for the airfield performance.
A constrained, and more realistic, optimum wing loading. is obtained if we postulate that the aircraft should cruise at Mcr =0.8 at a constant height h = 6km, so that qcr = 21kN/m^ also remains constant. The aircraft cannot then fly at the maximum value of L/D , and the fuel used will vary with the wing loading. The fuel fraction is given by the last term in (7.5), which can be rewritten in the form
|
R 1 |
R / °DF 1 c |
(7.7) |
||
|
Hr) (L/D) ‘p 4 ‘cr |
%VCLcr ^ Lcr/ |
9 |
||
|
where |
г _ W/S Lcr q * 4cr |
(7.8) |
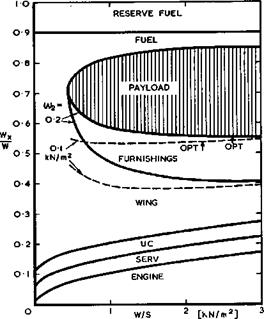
This can be inserted into (7.5) for the payload fraction, where the wing loading now appears in two further terms which again oppose each other. The optimum payload and wing loading must now be determined numerically. With the numbers used before, a typical weight breakdown is shown in Fig. 7.4, where the values of W/S which give the optimum payload are marked. According to this, the payload may Ъе as high as 30% of the all-ыр weight and thus better than that of corresponding aircraft of the classical type (see e. g. Figs. 4.3 and 4.4): a well-designed allwing aerobus presents a worthwhile target!
The constrained optimum payload is only slightly less than that corresponding to (7.6). We note further that the payload varies only little on either side of the optimum values of W/S so that there is quite some latitude in the choice of W/S, which may be used to satisfy other design requirements.
Fig. 7.4 also illustrates once more the incentive to reduce the other weight items, such as furnishings, to improve the economics. Again, an air-traffic control system which would allow a reduction of the reserve fuel would bring a worthwhile increase in payload.
In one of the examples in Fig. 7.4, the optimum wing loading is W/S = 2.8kN/m^. The thrust-to-weight ratio at take-off is then Tha/W = 0.56 , by (7.4). This is rather high, and implies that a high level of engine noise must be expected while the aircraft is on the runway. A longer runway than that assumed here would reduce Tha/W and hence the noise. But the engine may be throttled back after take-off. For example, (6.7) gives a climb-out speed Va = 95m/s at an angle 6a = 3° and CLa = 0.5 for Tha/W =0.22 . This reduction, together with the noise-shielding effects discussed in section 5.9, should make the allwing aerobus a quiet aircraft in flight.
LIVE GRAPH
Click here to view
|
Fig. 7.4 Weight breakdown of a family of slender allwing aircraft |