Prandtl Lifting Line Theory

15.4.2.1 Vortex Sheet

The vortex sheet is a stream surface originating at the sharp trailing edge of a finite wing. It is a surface of discontinuity of V. It has the following properties:

< u > = 0, no jump in u since pressure is continuous at the vortex sheet,

< w >= 0, no jump in w because the surface a zero thickness and the fluid is tangent to it (tangency condition)

< v >= 0, which can be related to the fact that the surface is made of vortex filaments of equation y = const., z = 0, 0 < x <ro.

15.4.2.2 Designing for Tip Vortices

Г[y(t)] = 2Ub{A1 sin t + A3 sin 3t}, where y(t) = -0.5b cos t, 0 < t < n.

Computing Г’ = (dГ/dt) / (dy/dt) shows that as, say, t ^ 0 the fraction is of the form 0/0. However, if dГ/dt ^ 0 faster than sin t a t, the result will be obtained.

dГ/dt = 2Ub{A1 cos t + 3A3 cos 3t}, thus, as t ^ 0 the necessary condition is A1 + 3A3 = 0. With this result, dГ/dt = 2UbA1{cos t – cos3t} a UbAtf2 as t ^ 0. The result is confirmed.

One finds A1 = (CL)t-o / (nAR) and A3 = – (CL)t-o / (3nAR).

The downwash is given by ww [y(t)] = —U {A1 +3 A3 sin3t / sin t }=-2UA1(1- 2 cos21). In terms of y this is ww(y) = -2UA1(1 – 2 (2y/b)2), a parabolic distri­bution. See Fig. 15.12.

The induced velocity ww is negative near the root, but there is upwash near the wing tips.

15.4.2.3 Induced Drag

The induced drag is given by Cm = nAR{A2 + 3A2} = (CDi)elliptic U + 332} = 4 (CDi )eiiiptic. There is a 33 % loss compared to the elliptic loading.

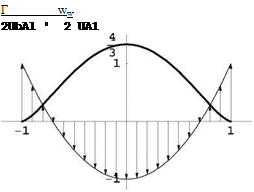Fig. 15.12 Circulation and downwash for the wing with weak tip vortices