14.8.3 Modern Identification Methods

The higher powered stability derivative extraction schemes that followed knob twisting engage the interest of many mathematically minded people in the stability and control community. The focus has been broadened beyond the linearized stability deriva­tives, and the subject is now usually called flight vehicle system identification. The years have seen centers of identification activity at individual laboratories, such as Calspan and the NASA Dryden Flight Research Center, and any number of university graduate students earning doctoral degrees in this area. Kenneth W. Iliff and Richard E. Maine at Dryden are leaders in the identification field in the United States.

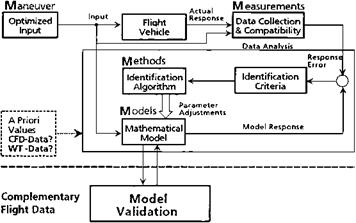
The DLR Institute in Braunschweig is particularly active in this area, under the guidance of Dr. Peter Hamel. The state of the art up to 1995 is summarized in a paper having 183 references by Drs. Hamel and Jategaonkar (1996). This summary has been updated (Hamel and Jategaonkar, 1999). A generalized model of the vehicle system identification process is shown in Figure 14.15.

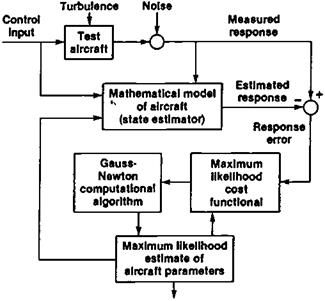
A flow chart for a widely used method known as the maximum likelihood or output error method is given in Figure 14.16. The maximum likelihood method starts with a mathematical model of the airplane, which is nothing more than the linearized equations of airplane motion in state variable form (see Chapter 18). The method produces numerical values for the constants in those equations, the airplane’s dimensional stability and control derivatives. A cost function is constructed as the difference between measured and estimated responses, summed over a time history interval. Iliff describes the workings of the maximum likelihood method as follows (see Figure 14.16):

Figure 14.15 The generalized method of vehicle system identification. (From Hamel, RTO MP-11, 1999)

Figure 14.16 Flow chart for the maximum likelihood method of airplane stability and control deriva­tive extraction from flight test data. (From Iliff, Jour, of Guidance, Sept.-Oct. 1989)

The measured response is compared with the estimated response, and the difference be­tween these responses is called the response error. The cost functions… include this response error. The minimization algorithm is used to find the coefficient values that minimize the cost function. Each iteration of this algorithm provides a new estimate of the unknown coefficients on the basis of the response error. These new estimates of the coefficients are then used to update values of the coefficients of the mathematical model, providing a new estimated response and, therefore, a new response error. The up­dating of the mathematical model continues iteratively until a convergence criterion is satisfied.

At the time of this writing, the maximum likelihood method is the most widely used of the available identification techniques. For example, in 1993, R. V Jategaonkar, W. Monnich, D. Fischenberg, and B. Krag used this method at the DLR, Braunschweig, for the Transall airplane; and M. R. Napolitano, A. C. Paris, and B. A. Seanor used it at West Virginia University for the Cessna U-206 and McDonnell Douglas F/A-18 airplanes. In an ear­lier use at the NASA Dryden Flight Research Facility, Iliff, Maine, and Mary F. Schafer used maximum likelihood estimation to get a fairly complete set of stability and control derivatives for a Cessna T-37B and a 3/8-scale drop model of the McDonnell Douglas F-15.

Identification quality is dependent on the frequency content of the control input signal in Figure 14.16. Ideal control inputs would excite the system’s modes of motion that require control, while leaving unexcited higher frequencies representing measurement artifacts, such as vibration. Koehler (1977) at DLR devised a simple input with a relatively wide, but limited, frequency content. This is the 3211 signal. The 3211 refers to alternate positive and negative pulses of relative durations 3,2, 1, and 1. The DLR 3211 signal has become a standard in vehicle systems identification.

The alternate extended Kalman filter method of stability derivative extraction has the advantage of being suited to real-time operation. That is, it can be used as an element in a

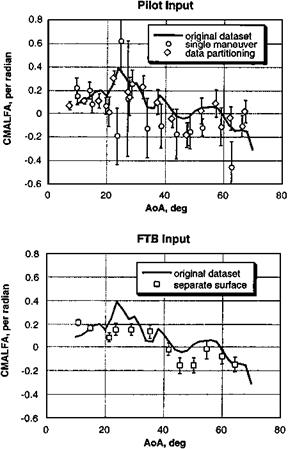
Figure 14.17 Improvement of Cma identification on the X-31A with separate surface inputs. (From Weiss, Jour, of Aircraft, 1996)

closed-loop flight control system. Many of the applications of extended Kalman filtering imply or use this feature, as in the 1983 to 1991 work at Princeton University by M. Sri- Jayantha, Dennis J. Linse, and Robert F. Stengel.

A challenging area for identification is that of the aerodynamically unstable airframe, which can be flown only with full-time stability augmentation. Data scatter can be large in these cases, using current methods. Figure 14.17 shows that exciting motion with a separate control surface from that used for closed-loop control reduces identification data scatter.

Rotary derivatives and cross-derivatives, such as the rolling moment due to yawing and the yawing moment due to aileron deflection, are generally the least well-known data in the airplane equations of motion. Identification methods are at their worst for such parameters. Correlations of extracted derivatives with wind-tunnel and theoretical data generally focus on just those derivatives such as Clp and Clp whose numerical values are well known from other sources. Flight test data quality must be high for identification algorithms to work well, probably higher than needed for any other application. State noise from atmospheric turbulence and sensor noise are obvious complications.

The power of flight vehicle system identification continues to advance to the point where the derived system models can meet accuracy requirements for high-fidelity flight

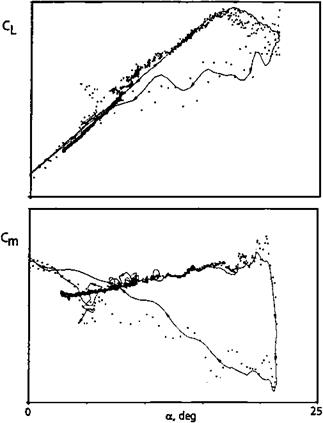
Figure 14.18 Unsteady aerodynamic modeling of approach to stall, stall, and recovery on the Do 328 transport. Dots are flight test data; solid line is model output. (From Fischenberg and Jategaonkar, RTO MP-11, 1999)

simulators, such as those used in research and pilot training. Recent extensions of the theory include using the frequency domain in place of the usual time domain methods, and the application of neural networks.