Circulation and the Topology of Flow Regimes

Most of the theorems and other results stated or derived in preceding portions of the chapter refer to finite bodies moving through a finite or infinite mass of liquid. If these bodies have no holes through them, such a field is simply connected in the sense that any closed circuit can be shrunk to a point or continuously distorted into any other closed circuit without ever passing outside the field.

A physical situation of slightly greater complexity, called doubly con­nected, is one where two, but no more than two, circuits can be found such that all others can be continuously distorted into one or the other of them. Examples are a single two-dimensional shape, a body with a single penetrating hole, a toroid or anchor ring, etc. Carrying this idea further, the flow around a pair of two-dimensional shapes would be triply con­nected, etc.

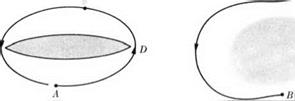
In the most general flow of a liquid or gas in a multiply connected region, Ф is no longer a single-valued function of position, even though the boundary conditions are specified properly as in the simply connected case. Turning to Fig. 2-6, let Фа be the specified value of the velocity potential at point A and at a particular instant. Then Фя can be written either as

or as

Фв2 = фл + [ Q • ds. (2-92)

Jadb

These two results will not necessarily be equal, since we cannot prove the identity of the two line integrals when the region between them is not entirely occupied by fluid. As a matter of fact, the circulation around the closed path is exactly

Г = <£ Q • ds = Фд2 — ФВі. (2-93)

JADBCA

It is an obvious result of Stokes’ theorem that Г is the same for any path completely surrounding just the body illustrated. Hence the differ­ence in the values of Ф taken between paths on one side or the other always turns out to be exactly Г, wherever the two points A and В are chosen.

Until quite lately it was believed that, to render constant-density fluid motion unique in a multiply connected region, a number of circulations must be prescribed which is one less than the degree of connectivity. A forthcoming book by Hayes shows, however, that more refined topological concepts must be employed to settle this question. He finds that the indeterminacy is associated with a topological property of the region known as the Betti number. Since the mathematical level of these ideas exceeds what is being required of our readers, we confine ourselves to citing the reference and asserting that it confirms the correctness of the simple examples discussed here and in the following section.

Consider the motion of a given two-dimensional figure S with Г = 0. A certain set of values of ЗФ/дп on S can be satisfied by a velocity potential representing the noncirculatory flow around the body. To this basic flow it is possible to add a simple vortex of arbitrary strength Г for which one

В

C

s

Fig. 2-6. Circuit drawn around a two – Fig. 2-7. An illustration of the circuit dimensional shape surrounded by fluid, implied in Eq. (2-94).

of the circular streamlines has been transformed conformally into precisely the shape of S. The general mapping theorem says that such a transforma­tion can always be carried out. By the superposition, a new irrotational flow has been created which satisfies the same boundary conditions, and it is obvious that uniqueness can be attained only by a specification of Г.

Leaving aside the question of how the circulation was generated in the first place, it is possible to prove that Г around any such body persists with time. This can be done by noting that the theorem of Kelvin, (1-12), is based on a result which can be generalized as follows:

(2-94a)

The fluid here may even be compressible, and A and В are any two points in a continuous flow field, regardless of the degree of connectivity. See Fig. 2-7. If now we bring A and В together in such a way that the closed path is not simply connected, and if we assume that there is a unique relation between pressure and density, we are led to

(2-94b)

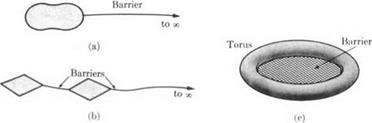
Let us now again adopt the restriction to constant-density fluid and examine the question of how flows with multiply connected regions and nonzero circulations might be generated. We follow Kelvin in imagining at any instant that a series of barriers or diaphragms are inserted so as to make the original region simply connected by the specification that no path may cross any such barrier. Some examples for which the classical results agree with Hayes are shown in Fig. 2-8.

The insertion of such barriers, which are similar to cuts in the theory of the complex variable, renders Ф single-valued. We recall the physical interpretation [cf. (2-15)]

Fig. 2-8. Three examples of multiply connected flow fields, showing barriers that can be inserted to make Ф unique. In (a) and (b), the shaded shapes are two­dimensional.

of Ф as the impulsive pressure required to generate a flow from rest. If such impulsive pressures are applied only over the surfaces of the bodies and the boundary at infinity in regions like those of Fig. 2-8, a flow without circulation will be produced. But suppose, additionally, that discontinuities in P of the amount

ДР = —p ДФ = – рГ (2-96)

are applied across each of the barriers. Then a circulation can be produced around each path obstructed only by that particular barrier. The genera­tion of a smoke ring by applying an impulse over a circular area is an obvious example. Note that ДФ (or Г) is constant all over any given barrier, but the location of the barriers themselves presents an element of arbi­trariness.