CLIMB ALONG INCLINED TRAJECTORY
§ 50. General Characteristics of the Climb Regime /10^
Along an Inclined Trajectory
Climb along an inclined trajectory is rectilinear flight of the helicopter with constant velocity and constant angle relative to the horizontal plane.
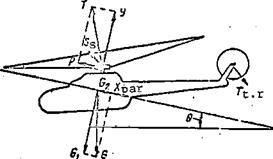
In this flight regime the helicopter is subject to the weight force, main rotor and tail rotor thrust forces, and the parasite drag force (Figure 67). To determine the flight conditions the helicopter weight force /10- can be broken down into components: G^ perpendicular to the flight path, and
G^ parallel to the flight path and directed opposite the motion.
The main rotor thrust force can also be resolved into the components Y (lift force), P (propulsive force), Sg (side force). The conditions for steady climb are expressed by the equalities
|
|
|
|
|
|
|
|
|
§ 51. Thrust and Power Required for Climb
The thrust required for climb can be found by using the diagram of the forces acting on the helicopter (Figure 67),
![]() (31)
(31)
where
Gi = G cos 0.; Gz — Gsin9.
|
magnitude G sin 0. Consequently, in (31) the first term of the radicand is smaller than in (26), while the second term is larger than the second term of (26). Therefore, the thrust required for climb along an inclined trajectory is practically the same as the thrust required for horizontal flight at the same speed.
![]() If a helicopter can hover, then it can climb along an inclined trajectory. This conclusion is confirmed by the fact that excess thrust appears in the forward flight regime (Figure 68). Consequently, even with some thrust deficiency for hovering (dashed curve in Figure 68), climb along an inclined trajectory at a speed greater than the minimal horizontal flight speed is possible. This circumstance is utilized in the running helicopter takeoff.
If a helicopter can hover, then it can climb along an inclined trajectory. This conclusion is confirmed by the fact that excess thrust appears in the forward flight regime (Figure 68). Consequently, even with some thrust deficiency for hovering (dashed curve in Figure 68), climb along an inclined trajectory at a speed greater than the minimal horizontal flight speed is possible. This circumstance is utilized in the running helicopter takeoff.
The power required for climb is found from the same formula as used to find the power required for horizontal flight
But in this formula the terms may differ from the corresponding terns for the power required for horizontal flight.
During climb N will not differ from the profile power for horizontal flight if the rpm and flight speed are the same.
The induced power in climb is practically equal to the induced power for
»
horizontal flight, since
N. = YV., and Y, = G cos 0 % G. і і cl
But the power required for motion during climb differs considerably from the motion power for horizontal flight
N t = PV = (X + G.) V = X V. + G. V..
mot cl par 2 cl par cl 2 cl
= N „ + AN.
![]() mot, h
mot, h
Climb is possible if there is excess power AN (i. e., the power available exceeds the power required for horizontal flight)
![]()
 |
N = N, + AN. cl h