Compensatory Operation and Model Categories

Pilot-in-the-loop analysis methods have had their earliest and most meaningful successes representing compensatory operation. As applied to pilot-in-the-loop operation, in compensatory operation or tracking the pilot operates on displayed or perceived errors to minimize them in a closed-loop fashion. Precognitive pilot operation is essentially open – loop; the pilot is not part of the tracking loop.

Mathematical models for pilot compensatory operation fall into two categories, struc­tural and algorithmic. Structural models reduce the pilot to subsystems such as muscle manipulators and vestibular sensors, each with transfer functions. Structural model pilot transfer functions contain delays, leads, and lags. The overall assemblage must reproduce pilot behavior in an end-to-end fashion. This challenging approach is made possible by careful frequency response measurements on human subjects (McRuer, 1973).

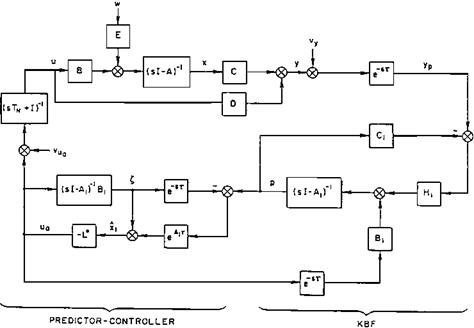
Pilot algorithmic models have grown out of modern optimal control theory. These models include an estimator, such as a Kalman filter, which processes the pilot’s observations to provide an estimate of the airplane’s state, and a controller, which is a mathematical model for the pilot’s regulation and muscular functions (Figure 21.2). Minimization or maximization of a criterion function provides the required results.

It is important to recognize that delay-lead-lag pilot models are needed primarily in analysis of compensatory operation of inner, generally attitude loops. Such loops are closed at high frequencies relative to pilot dynamics. Pure gain models for the pilot are generally adequate for analysis of turn coordination and lower frequency speed and path control loops.