Dimensional Analysis: The Buckingham Pi Theorem

The aerodynamic forces and moments on a body, and the corresponding force and moment coefficients, have been defined and discussed in Section 1.5. Question: What physical quantities determine the variation of these forces and moments? The answer can be found from the powerful method of dimensional analysis, which is introduced in this section.3

Consider a body of given shape at a given angle of attack, e. g., the airfoil sketched in Figure 1.10. The resultant aerodynamic force is R. On a physical, intuitive basis, we expect R to depend on:

1. Freestream velocity Voo.

2. Freestream density Poo.

3. Viscosity of the fluid. We have seen that shear stress r contributes to the aero­dynamic forces and moments. In turn, in Chapter 15, we will see that r is proportional to the velocity gradients in the flow. For example, if the velocity gradient is given by du/dy, then r = /іди/ду. The constant of proportionality is the viscosity coefficient fi. Hence, let us represent the influence of viscosity on aerodynamic forces and moments by the freestream viscosity coefficient fi<*,.

4. The size of the body, represented by some chosen reference length. In Figure 1.10, the convenient reference length is the chord length c.

5. The compressibility of the fluid. The technical definition of compressibility is given in Chapter 7. For our present purposes, let us just say that compressibility is related to the variation of density throughout the flow field, and certainly the aerodynamic forces and moments should be sensitive to any such variation. In turn, compressibility is related to the speed of sound a in the fluid, as shown in Chapter 8.4 Therefore, let us represent the influence of compressibility on aerodynamic forces and moments by the freestream speed of sound, ax.

3 For a more elementary treatment of dimensional analysis, see Chapter 5 of Reference 2.

4 Common experience tells us that sound waves propagate through air at some finite velocity, much slower than the speed of light; you see a flash of lightning in the distance, and hear the thunder moments later. The speed of sound is an important physical quantity in aerodynamics and is discussed in detail in Section 8.3.

In light of the above, and without any a priori knowledge about the variation of R, we can use common sense to write

R — f (Pco, Fqo, C, fJ, oc, r^oc)

Equation (1.23) is a general functional relation, and as such is not very practical for the direct calculation of R. In principle, we could mount the given body in a wind tunnel, incline it at the given angle of attack, and then systematically measure the variation of R due to variations of px, V^, с, /xTO, and ax, taken one at a time. By cross-plotting the vast bulk of data thus obtained, we might be able to extract a precise functional relation for Equation (1.23). However, it would be hard work, and it would certainly be costly in terms of a huge amount of required wind-tunnel time. Fortunately, we can simplify the problem and considerably reduce our time and effort by first employing the method of dimensional analysis. This method will define a set of dimensionless parameters which governs the aerodynamic forces and moments; this set will considerably reduce the number of independent variables as presently occurs in Equation (1.23).

Dimensional analysis is based on the obvious fact that in an equation dealing with the real physical world, each term must have the same dimensions. For example, if

ф + г} + ї =Ф

is a physical relation, then ifr, t], £, and ф must have the same dimensions. Oth­erwise we would be adding apples and oranges. The above equation can be made dimensionless by dividing by any one of the terms, say, ф:

These ideas are formally embodied in the Buckingham pi theorem, stated below without derivation. (See Reference 3, pages 21-28, for such a derivation.)

Buckingham pi theorem. Let К equal the number of fundamental dimensions required to describe the physical variables. (In mechanics, all physical variables can be expressed in terms of the dimensions of mass, length, and time’, hence, К = 3.)

Let P, P2, ■ ■ ■, PN represent N physical variables in the physical relation

fi(Pi, P2,…,PN)= 0

Then, the physical relation Equation (1.24) may be reexpressed as a relation of (N — K) dimensionless products (called П products),

/2(П,,П2……….. Пм) = 0

where each П product is a dimensionless product of a set of К physical variables plus one other physical variable. Let P, P2, …, Pk be the selected set of К physical variables. Then

n, = h(Pi, P2,…,PK, PK+,) П2 = f4(Pi, P2,…, PK, PK+2)

П/1-r — fs{P, P2, ■ ■ ■, Pk, Pn)

The choice of the repeating variables, P, P2, ■ ■ ■, Pk should be such that they include all the К dimensions used in the problem. Also, the dependent variable [such as R in Equation (1.23)] should appear in only one of the П products.

Returning to our consideration of the aerodynamic force on a given body at a given angle of attack, Equation (1.23) can be written in the form of Equation (1.24):

§(R> Росі koo> C, oo, ttoo) — 0 [1 *27]

Following the Buckingham pi theorem, the fundamental dimensions are

m = dimensions of mass l = dimension of length t = dimension of time

Hence, К — 3. The physical variables and their dimensions are

[R] = mlt~2 iPod = ml~3

[Vco]=/r-1
[c] = l

[доо] = ml~xt~l

[floo] = If1

Hence, N = 6. In the above, the dimensions of the force R are obtained from Newton’s second law, force = mass x acceleration; hence, [RJ = mlt~2. The dimensions of p. x are obtained from its definition, e. g., i =■ т/(ди/ду), and from Newton’s second law. (Show for yourself that [доо] = ml~lt~x.) Choose px, and c as the arbitrarily selected sets of К physical variables. Then Equation (1.27) can be reexpressed in terms of N — К = 6 — 3 = 3 dimensionless П products in the form of Equation (1.25);

/2(ПьП2,Пз) = 0 [1.28]

From Equation (1.26), these П products are

Пі =f3(p0O, V00,c, R) [1.29a]

П2 — /4(Roo 1 кос5 f, Доо) [ 1.298]

П3 = /5(Poo, ^ocChOoc) [1.29c]

For the time being, concentrate on Пь from Equation (1.29a). Assume that

Пі =piV^ceR [1.30]

where d, b, and e are exponents to be found. In dimensional terms, Equation (1.30) is

Because П, is dimensionless, the right side of Equation (1.31) must also be dimen­sionless. This means that the exponents of m must add to zero, and similarly for the exponents of / and t. Hence,

Form: d. + 1=0

For/: -3d + b + e + 1 = 0

For t: – b – 2 = 0

Solving the above equations, we find that d — – l, b — -2, ande = -2. Substituting these values into Equation (1.30), we have

Пі = fip^V"2^2 [1.32]

_ R ~ PooVfr*

The quantity R/px F^c2 is a dimensionless parameter in which c2 has the dimensions of an area. We can replace c2 with any reference area we wish (such as the planform area of a wing S), and Пі will still be dimensionless. Moreover, we can multiply Пі by a pure number, and it will still be dimensionless. Thus, from Equation (1.32), П! can be redefined as

Hence, Пі is a force coefficient CR, as defined in Section 1.5. In Equation (1.33), S is a reference area germane to the given body shape.

The remaining П products can be found as follows. From Equation (1.29b), assume

n2 = /OooV£c’V [1.34]

Paralleling the above analysis, we obtain

[П21 = (тГ3)(Іг’У’(іУ(тГ’г1У

Hence,

Form: 1 + j — 0

For/: —3 + h + i— j = 0

For t: – h – j — 0

Thus, j = — 1, h = 1, and і = 1. Substitution into Equation (1.34) gives

The dimensionless combination in Equation (1.35) is defined as the freestream Rey­nolds number Re = Poo Vooc/P-ao – The Reynolds number is physically a measure of the ratio of inertia forces to viscous forces in a flow and is one of the most powerful parameters in fluid dynamics. Its importance is emphasized in Chapters 15 to 20.

Returning to Equation (1.29c), assume

n3 = Voo p^c’a^

[П3] = (ІГ1)(тГ3)к(.іУ(ІГ1У

For m: к — О

For 1: 1— 3fc + r + s = 0

For P. — 1 — s = 0

Hence, к = 0, s = — 1, and r = 0. Substituting Equation (1.36), we have

Пе = — [1.37]

floo

The dimensionless combination in Equation (1.37) is defined as the freestream Mach number M = Vqo/Ooo – The Mach number is the ratio of the flow velocity to the speed of sound; it is a powerful parameter in the study of gas dynamics. Its importance is emphasized in subsequent chapters.

The results of our dimensionless analysis may be organized as follows. Inserting Equations (1.33), (1.35), and (1.37) into (1.28), we have

fi(CR, Re, Moo) = 0

This is an important result! Compare Equations (1.23) and (1.38). In Equation (1.23), R is expressed as a general function of five independent variables. However, our dimensional analysis has shown that:

1. R can be expressed in terms of a dimensionless force coefficient,

cR = R/Poovls.

2. CR is a function of only Re and M„, from Equation (1.38).

Therefore, by using the Buckingham pi theorem, we have reduced the number of independent variables from five in Equation (1.23) to two in Equation (1.38). Now, if we wish to run a series of wind-tunnel tests for a given body at a given angle of attack, we need only to vary the Reynolds and Mach numbers in order to obtain data for the direct formulation of R through Equation (1.38). With a small amount of analysis, we have saved a huge amount of effort and wind-tunnel time. More importantly, we have defined two dimensionless parameters, Re and М^, which govern the flow. They are called similarity parameters, for reasons to be discussed in the following section. Other similarity parameters are introduced as our aerodynamic discussions progress.

Since the lift and drag are components of the resultant force, corollaries to Equa­tion (1.38) are

Cl = /7 (Re, Mx) [1.39]

CD = MRe, Moo) [1.40]

Moreover, a relation similar to Equation (1.23) holds for the aerodynamic moments, and dimensional analysis yields

CM = /9(Re, Mx) [1.41]

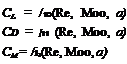Keep in mind that the above analysis was for a given body shape at a given angle of attack a. If a is allowed to vary, then CL, CD, and CM will in general depend on the value of a. Hence, Equations (1.39) to (1.41) can be generalized to

Equations (1.42) to (1.44) assume a given body shape. Much of theoretical and experimental aerodynamics is focused on obtaining explicit expressions for Equations (1.42) to (1.44) for specific body shapes. This is one of the practical applications of aerodynamics mentioned in Section 1.2, and it is one of the major thrusts of this book.

For mechanical problems that also involve thermodynamics and heat transfer, the temperature, specific heat, and thermal conductivity of the fluid, as well as the tem­perature of the body surface (wall temperature), must be added to the list of physical variables, and the unit of temperature (say, kelvin or degree Rankine) must be added to the list of fundamental dimensions. For such cases, dimensional analysis yields additional dimensionless products such as heat transfer coefficients, and additional similarity parameters such as the ratio of specific heat at constant pressure to that at constant volume cp/cv, the ratio of wall temperature to freestream temperature Tw/Too, and the Prandtl number Pr = k^_. where кж is the thermal conduc­

tivity of the freestream.[3] Thermodynamics is essential to the study of compressible flow (Chapters 7 to 14), and heat transfer is part of the study of viscous flow (Chapters 15 to 20). Hence, these additional similarity parameters will be emphasized when they appear logically in our subsequent discussions. For the time being, however, the Mach and Reynolds numbers will suffice as the dominant similarity parameters for our present considerations.