Dynamics Relations

9.7.1 Linear momentum

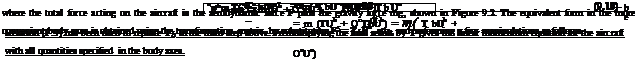
The linear momentum equation (Newton’s Second Law) for an aircraft, properly expressed in the inertial Earth frame and Earth axes is

9.7.2 Angular momentum

The angular momentum equation for the aircraft is

d Hb

Me = —— (9.20)

d t

— b

Hb = I Ob + hb (9.21)

where the total angular momentum vector H has been introduced, with h being any onboard angular mo­mentum due to propellers, turbines, etc. The total aerodynamic moment M, shown in Figure 9.2, is assumed to be taken about the center of mass, and I is the mass moment of inertia about the center of mass. To put the angular momentum equation (9.20) in the more convenient body axes, we follow the same procedure as for the linear momentum equation above, except that F is now replaced by M, and mU is replaced by H.

TbMb = ^(TbHb)

= Tb Hb + (n x H)b

Premultiplying the final result by Tb, and then replacing Hb by I fib + hb gives the angular momentum equation for the aircraft in body axes.