Examples of Two – and Three-Dimensional Flows Without Circulation

We now look at some simple illustrations of constant-density flows without circulation, observe how the mathematical solutions are obtained, how virtual masses are determined, and how other information of physical interest is developed.

1. The Circular Cylinder. It is well known that a circular cylinder of radius c in a uniform stream Ux parallel to the negative ж-direction is represented by the velocity potential

(2-75)

Here r and в are conventional plane polar coordinates, and the cylinder is, of course, centered at their origin.

If we remove from this steady flow the free-stream potential

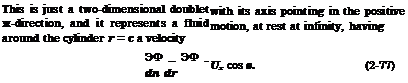This result can be regarded as describing the motion for all time in a set of portable axes that move with the cylinder’s center. Moreover, the velocity U„ may be a function of time.

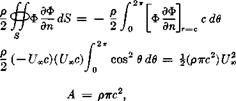Per unit distance normal to the flow, the kinetic energy of the fluid is

whereas the inertia coefficient В would have the same value and all other coefficients in the r, 0-plane must vanish. We reach the interesting, if accidental, conclusion that the virtual mass of the circular cylinder is precisely the mass of fluid that would be carried within its interior if it were hollowed out. This mass is the factor of proportionality which would relate an ж-acceleration to the inertial force of resistance by the fluid to this acceleration.

These same results might be obtained more efficiently using the complex variable representation of two-dimensional constant-density flow, as dis­cussed in Sections 2-9 ff.

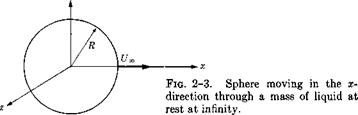
2. Sphere of Radius R Moving in the Positive x-Direction (Fig. 2-3).

With the fluid at rest at infinity, the sphere passing the origin of coor­dinates at time t = 0 and proceeding with constant velocity Ux has the instantaneous equation, expressed in coordinates fixed to the fluid at infinity,

B(x, y, z, t) = (ж — UJ)2 + y2 + z2 — R2 = 0. (2-80)

The boundary condition may be expressed by the requirement that В is a constant for any fluid particle in contact with the surface. That is,

T)D

^ = 0 on В = 0. (2-81)

Working this out with the use of (2-80),

In this example we proceed by trial, attempting to satisfy this condition at t = 0 by means of a doublet centered at the origin with its axis in the positive ж-direction,

Hx 4 жг3

We calculate the velocity components

If (2-85а), (b), and (с) are inserted into (2-82), and r and t are set equal to R and 0, respectively, we are led after some algebra to a formula for the strength H of the doublet:

H = 2irR3Ux. (2-86)

The uniqueness theorem, asserted earlier in the chapter, assures that we have the correct answer.

2ttR3Uxx _ _ U„x R3 4irr3 2 r3

As in the case of the circular cylinder, all kinds of information can be readily obtained once the velocity potential is available. By adding the potential of a uniform stream Ux in the negative ж-direction one con­structs the steady flow and can then obtain streamlines and velocity and pressure patterns around the sphere. The only inertia coefficients are direct virtual masses. It is also of interest that the unsteady potential dies out at least as fast as the inverse square of distance from the origin when

one proceeds toward infinity, and the velocity components die out at least as the inverse cube. General considerations lead to the result that the disturbance created in a constant-density fluid by any nonlifting body will resemble that of a single doublet at remote points.

The foregoing example of the sphere is just a special case of a more general technique for constructing axially symmetric flows around bodies of revolution by means of an equilibrating system of sources and sinks along the axis of symmetry. (The doublet is known to be the limit of a single source-sink pair.) This procedure was originally investigated by Rankine, and such figures are referred to as Rankine ovoids. Among many other investigators, von Karmdn (1927) has adapted the method to airship hulls.

For blunt shapes like the sphere, the results of potential theory do not agree well with what is measured because of the presence of a large sep­arated wake to the rear, a problem which we discuss further in Chapter 3. It was this sort of discrepancy that dropped theoretical aerodynamics into considerable disrepute during the nineteenth century. The blunt-body flows are described here principally because they provide simple illustra­tions. When it comes to elongated streamlined shapes, a great deal of useful and accurate information can be found without resort to the non­linear theory of viscous flow, however, and such applications constitute the ultimate objective of this book.

Fig. 2-4. Prolate ellipsoid of revolu­tion moving through constant-density fluid at an angle of attack a in the x, y- plane.

3. Ellipsoids. A complete account of the solution of more complicated boundary-value problems on spheres, prolate or oblate ellipsoids of revolu­tion, and general ellipsoids will be found in the cited references. Space considerations prevent the reproduction of such results here, with the exception that a few formulas will be given for elongated ellipsoids of revolution translating in a direction inclined to the major axis. These have considerable importance relative to effects of angle of attack on fuselages, submarine hulls, and certain missile and booster configurations.

For the case shown in Fig. 2-4, the velocity

u = if/», cos a + jUx sin a gives rise to a Kelvin impulse f = ІAUoo cos a + jBUa sin a

The ellipsoid’s volume is, of course, §7гаЬ2, whereas the dimensionless coefficients

[«o/(2 — ao)L [do/(2 /So)]

are functions of eccentricity tabulated in Section 115 of Lamb (1945).

With constant speed and incidence the force is zero, but the vectors u and £ are not quite parallel and an overturning couple is generated,

Mbody = – uXf

– – k v – – 5^} ™ 2«; (2-90)

the inertia factor here in braces is always positive, vanishing for the sphere. At fineness ratios above ten it approaches within a few percent of unity. Thus the familiar unstable contribution of the fuselage to static stability is predicted theoretically. The calculations are in fairly satisfactory accord with measurements when a/b exceeds four or five. Figure 2-5 presents a comparison with pitching-moment data.