Flexural Response and Interior Sound Radiation of a Closed Shell Excited by a TBL Pressure Field

This section introduces a general formulation for the interior noise in a cavity bounded by a flexible wall, which is excited by the space and time stochastic pressure field exerted by a “Turbulent Boundary Layer” (TBL) relative fluid flow (for brevity, the fact that the fluid flow is relative to the wall structure will not be specified in the remaining part of this chapter). A coupled structural- acoustic formulation is presented considering a cylindrical cavity of finite length bounded by a thin flexible wall, which is assumed to be simply-supported at the two ends. As illustrated in Figure 1, the cylindrical flexible wall is connected to rigid extensions acting as baffles and is immerged in an unbounded fluid. The fluid is convected in axial direction and produces a fully developed TBL over the wall. Although this model problem can be used to study a limited number of practical systems, it provides general indications of the principal mechanisms characterising the TBL excitation, response and radiation phenomena of the complex enclosures that are encountered in surface and air passenger transportation vehicles (Mixson and Wilby 1995; Thompson and Dixon 2004).

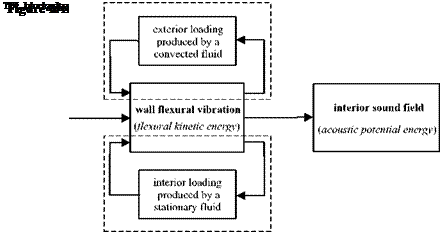As schematically depicted in Figure 2, the interior sound radiation is produced by the flexural vibration of the enclosing wall, which depends on the resulting pressure fields acting on the inner and outer faces of the wall. The pressure field on the inner face is due to the interior sound field, which, in turn, depends on the flexural vibration of the enclosing wall itself. Normally, at low audio frequencies, the interior sound is characterised by standing wave fields due to the low order acoustic natural modes of the enclosure. Alternatively, at higher frequencies the interior sound field becomes increasingly diffuse since, at each frequency, the acoustic response of the enclosure results from the overlap of multiple acoustic modes whose number grows with the cube of frequency (Morse and Ingard 1968; Pierce 1989; Nelson and Elliott 1992; Fahy and Gardonio 2007). Usually the transition from standing wave to diffuse sound field is specified in terms of the “modal overlap” factor, which depends on the “modal density” and damping properties of the cavity (Cremer et al. 1988). At low frequencies where the acoustic response of the enclosure and the vibration response of the shell structure are characterised by distinct resonant modes, the interior fluid loading effect is normally formulated in terms of modal coupling

factors (Dowell and Voss 1962; Pretlove 1966; Fahy 1969; Guy and Bhattacharya 1973). Alternatively, at higher frequencies such that the acoustic and structural responses are controlled by the overalp of multiple modes, the fluid loading is modelled in average terms through coupling factors for “statistical energy analysis” models (Lyon and DeJong 1995; Craik 1996; Keane and Price 1997; Langley and Fahy 2004; Fahy and Gardonio 2007). In general, the interior of surface and air transportation vehicles is filled with air, i. e. a lightweight compressible fluid. As further detailed in Section 1.5, in this case the interior fluid loading primarily produces a damping action.

The pressure field on the outer face of the wall structure is characterised by two contributions: first, the pressure field produced by the TBL fluid flow over the flexible wall and second the acoustic pressure field due to the exterior sound radiation produced by the vibration of the flexible wall itself. As discussed in Chaper 6 of this book, the TBL fluid flow produces a stochastic pressure field over the external surface of the wall, which, in general, is also influenced by the flexural vibration of the wall (Graham 1997; Maury et al. 2002a). However, in this chapter, the so called “blocked pressure” field is considered, which corresponds to the pressure developed beneath a boundary layer on a hard wall. In this case the pressure generated by the TBL fluid flow is not affected by the flexural vibration of the wall and it is twice the pressure that a nominally identical turbulent fluid flow would generate in absence of the wall. This assumption is valid when the TBL is fully developed and the acoustic near field particle velocities produced by flexural vibration of the wall are small in comparison with the turbulence particle velocities (Graham 1997; Maury et al. 2002a). This type of approximation has been found valid in a wide range of cases as detailed in the following references, for example (Davies 1971; Efimtsov and Shubin 1977; Efimtsov 1986; Bano et al. 1992). A fully coupled model would require a rather complex formulation, using the Lighthill stress tensor to describe the boundary layer sources (Dowling and Ffowcs Williams 1983). The outward sound radiation due to the wall flexural vibration also produces a pressure field over the surface of the shell structure. In general, the exterior of surface and air transportation vehicles is characterised by air (i. e. lightweight compressible fluid), which, as will be shown in Section 1.5, for low flow speeds, tends to produce a damping fluid loading effect arising from the sound radiation into a fully or partially unbounded field (Junger and Feit 1986; Fahy and Gardonio 2007). However, the cruise speed of aircraft for passenger transportation approaches rather high values, around 0.8 Mach. In this case the flexible skin structure efficiently couples with the fluid dynamic response and gives rise to the so called “aeroelastic coupling” (Dowell 1975; Abrahams 1983; Lyle and Dowell 1994; Atalla and Nicolas 1995; Clark and Frampton 1997; Frampton and Clark 1997; Frampton 2005; Xin and Lu 2010). Clark and Frampton (Clark and

Frampton 1997; Frampton and Clark 1997; Frampton 2005) have shown that, for high flow speeds around 0.8 Mach, the convected fluid produces damping and increasingly higher mass impedance effects on the structure that tend to reduce the amplitude and to move to lower frequencies the resonance peaks that characterise the low-frequency spectrum of the flexural response of the enclosing wall structure. The aeroelastic response of shell structures is a rather complex non-linear phenomenon that involves strong coupling effects between low order flexural modes of the wall panels via the dynamics of the mean flow. Eventually, for very large flow velocities that exceed the speed of sound, this coupling effect may lead to limit cycle modal vibrations and thus to flutter instability conditions (Dowell 1975). Of course, flutter is of no concern for the skin panels of modern aircraft. Nevertheless, for high flow speeds approaching 0.8 Mach, the dynamic coupling between the panels and the fluid has a relevant effect on the response of the shell structure and interior sound radiation. The scope of this chapter is to introduce the principal characteristics of interior sound radiation produced by TBL disturbances. Thus, although the model problem considered in this section also refers to fast moving air transportation vehicles, to keep the analysis simple, the proposed formulation does not take into account aeroelastic coupling. However it considers the fluid loading effect arising from sound radiation into a stationary fluid, which can be assumed valid for flow velocities below 0.8 Mach. This formulation provides a good basis for the understanding of the physical mechanisms characterising the coupling of structural modes via the exterior fluid loading. In general, a high velocity mean flow tends to emphasise these coupling effects so that, even with lightweight compressible fluids, strong couplings between low order modes of the wall structure may emerge (Clark and Frampton 1997; Frampton and Clark 1997; Frampton 2005). In summary the model presented in this chapter considers the flexural response and interior sound radiation of a closed shell structure, which is excited by the blocked pressure field exerted by a TBL fluid flow and is influenced by the acoustic loading effects exerted by the interior and exterior fluids.

Much of the analytical work on the structural-acoustic response to TBL fluid flow excitation is organised around two types of models: the first is based on space-frequency domain formulations (Dyer 1959; Mead and Richards 1968; Crocker 1969; Davies 1971; Robert 1984; Blake 1986; Masson 1991; Bano et al. 1992; Filippi and Mazzoni 1994; Thomas and Nelson 1995; Durant et al. 2000), while the second is based on wavenumber-frequency domain formulations (Aupperle and Lambert 1973; Blake 1986; Hwang and Maidanik 1990; Strawderman 1990; Graham 1996; Borisyuk and Grinchenko 1997; Graham 1997; Han et al. 1999; Maury et al. 2002a). The first modelling approach uses the space-frequency spectra of the pressure fields exerted by the internal and external fluids and by the TBL fluid flow, which, as discussed in Chapter 6, was introduced by Corcos (Corcos 1963a; Corcos 1963b; Corcos 1967). The second is instead based on the wavenumber-frequency spectra of the pressure fields exerted by the internal and external fluids and by the TBL fluid flow. As discussed in Chapter 6, over the past three decades a selection of analytical or quasi-analytical models have been proposed in the attempt of describing the spectrum of TBL pressure fields both at convective and sub-convective wavenumbers (Chase 1980; Efimtsov 1982; Ffowcs Williams 1982; Chase 1987; Smol’yakov and Tkachenko 1991; Bull 1995; Graham 1997). Maury et al. (2002a) have analysed the principal characteristics of the space-frequency and wavenumber-frequency formulations in a consistent framework and have highlighted how the two formulations are related by spatial Fourier transforms.

As seen for the interior sound field, in general, at low audio frequencies the response of the wall structure is also characterised by a low modal overlap. Thus the expression of the flexural vibration field can be expanded into a series of modal terms with reference to the in vacuo natural modes of the structure. In this case both formulations in the space and wavenumber domains lead to double series modal expressions for the structural response and sound radiation, which include the self and mutual admittance functions for the modal excitation exerted by the TBL pressure field, the self and mutual fluid loading impedance functions and the self and mutual sound radiation efficiencies (Davies 1971; Blake 1986). With the space-frequency domain formulation, the modal excitation, fluid loading and sound radiation effects are derived from integral expressions in a bounded space domain. Alternatively, for the wavenumber-frequency domain formulation, these terms are derived from integral expressions in the unbounded wavenumber domain. Although the two approaches provide equivalent results, the formulation in the space-frequency domain is more intuitive to derive since it refers to spatial coordinates (Blake 1986; Thomas and Nelson 1995; Maury et al. 2002a). Nevertheless, with the wavenumber-frequency domain formulation, the expressions for the modal excitation, fluid loading and sound radiation effects are transformed into wavenumber spectra. Thus the response of the structure can be viewed as the result of filtering phenomena between the wavenumber spectra of the modal excitation, the interior and exterior modal fluid loading and the interior modal sound radiation (Blake 1986; Hwang and Maidanik 1990; Graham 1997). This provides direct insight on the physics of the excitation, fluid loading and interior sound radiation phenomena under study, although working in the wavenumbers domain requires some practice. Both types of approaches are based on double integrations, which, in general, cannot be solved analytically and thus involve numerical derivation using, for example, the Gaussian quadrature. The wavenumber approach offers some advantages when the geometry of the structure can be defined in terms of a single coordinate with reference to systems of orthogonal coordinates in which the structural vibration field, the interior sound pressure field and the exterior sound and TBL pressure fields are separable. In this case, the wavenumber integral expressions can be derived analytically in closed form (Junger and Feit 1986; Fahy and Gardonio 2007). On the other hand the spatial approach can be easily implemented when the vibration response of complex structures and the interior and exterior sound fields are derived with approximated methods such as the structural and acoustic “Finite Element Method” (FEM) and the acoustic “Boundary Element Method” (BEM) (Filippi and Mazzoni 1994). At high audio frequencies the structural response and the interior sound field increasingly become complex, since multiple resonant modes contribute to both the vibration and sound fields at each frequency. Thus alternative formulations based on energy functions are employed such as the “Statistical Energy Analysis” (SEA) method. This chapter considers only the modal formulation, which for simple model problems, such as the cylindrical enclosure considered in this section or the baffled panel considered in the following sections, provides realistic results also at high audio frequencies.

In summary this section introduces the space-frequency domain formulation for the structural-acoustic response to TBL fluid flow excitations. Also, it briefly discusses the derivation of the modal excitation functions in the wavenumber- frequency domain. The reader interested to know more about “full” wavenumber-frequency domain formulations is referred to the review papers by (Graham 1997; Maury et al. 2002a) and to the monograph chapters written by (Blake 1986). The space-frequency domain formulation presented here is built around the description of the interior and exterior sound fields and the modal representation of the distributed flexural vibration of thin shells. In general, the interior and exterior sound fields can be derived with the so called “direct boundary integral formulation”, which uses acoustic Green functions (Morse and Ingard 1968; Blake 1986; Junger and Feit 1986; Pierce 1989; Nelson and Elliott 1992; Fahy and Gardonio 2007). For the exterior fluid domain, this equation provides the resultant sound field produced by a distribution of acoustic sources and by the radiation and scattering effects of a flexible body (or multiple bodies) of arbitrary shape. Alternatively, for the interior fluid domain, it provides the resultant sound field produced inside the enclosure by a distribution of interior acoustic sources and by the radiation and reflection effects of the enclosure flexible walls. The effects produced by the surface of the body or enclosure are normally classified in terms of three different boundary conditions that prescribe a) the velocity distribution normal to the boundary surface (Neumann or natural boundary condition), b) the sound pressure acting on the boundary surface (Dirichlet or essential boundary condition) and c) the specific acoustic impedance normal to the boundary surface (mixed boundary condition) (Ciskowski and Brebbia 1991; Desmet 1998; Wu 2000; Gaul et al. 2003). In general, when the boundary surface is defined by a flexible structure, the boundary conditions for both the exterior and interior noise problems are expressed in terms of the acoustic particle velocity distributions normal to the boundary surface, which are considered compatible with the transverse vibration velocity of the flexible wall. Thus they are treated as Neumann boundary conditions. The boundary integral formulation involves a surface integration that can be solved in closed form only for few regular shapes (e. g. cylinders and spheres). For more realistic irregular boundary surfaces, approximated numerical methods are employed such as the acoustic “Boundary Element Method” (BEM) or the acoustic “Finite Element Method” (FEM) (Wu 2000; Fahy and Gardonio 2007). Although the two methods can be used for both interior and exterior sound problems, normally the BEM method is used for the exterior sound radiation/scattering problem, while the FEM method is employed for the interior sound radiation/reflection problem.

For simple wall structures either formed by a single span shell or an assembly of plate and shell panels, the flexural response can be derived analytically from the inhomogeneous equations of motion for closed shells or flat and curved panels. The flexural response is derived in terms of structural Green functions, which, are usually expressed as admittance or mobility functions (Gardonio and Brennan 2002; Gardonio and Brennan 2004). Also in this case, for distributed pressure field excitations, the expression for the response assumes an integral form over the surface of the structure. In general, only for very few simple structures, such as for example cylinders or flat and curved rectangular panels, the flexural response can be derived analytically. In practice, the body of surface and air vehicles are rather complex structures. Thus, as for the acoustic problem, approximated numerical methods are normally employed such as the structural FEM (Fahy and Gardonio 2007). When the analysis is limited to low audio frequencies, the problem is often simplified by considering a simple closed wall structure (e. g. a cylinder or a folded box) where the stiffening and mass effects of the reinforcing ribs are smeared over the surface of the structure. Alternatively, at mid and high audio frequencies, the response of different sections of the enclosure wall can be considered weakly coupled to each other and thus the problem can be split into the analysis of the structural-acoustic response of single span flat panels and curved shells.

As schematically shown in Figure 2, the coupled structural-acoustic analysis presented in this section is derived by combining the acoustic responses of the interior and exterior sound fields and the structural response of the flexible wall. The flexural response of the wall produced by the TBL pressure field and by the feedback effects exerted by sound pressure fields over the internal and external surfaces of the wall is derived from the structural equation of motion. The sound
pressure over the internal and external surfaces are derived from the direct boundary integral equations for the interior and exterior sound fields calculated on the boundary surface. The structural equation of motion and the direct boundary integral equations are then combined into a system of equations in the unknown sound pressure and particle velocity fields over the boundary surface. The resulting sound pressure and particle velocity fields are then used again in the direct boundary integral equation for the interior sound field to derive the noise radiation inside the enclosure.

To effectively establish the interior sound radiation and global flexural response of a cavity bounded by flexible walls, it is convenient to express the two phenomena in terms of energy functions, which embrace in a single term the spatially distributed nature of the sound and flexural vibration fields in the cavity and enclosing wall respectively (Nelson and Elliott 1992; Gardonio 2012). Moreover, the stochastic nature of the disturbance pressure field exerted by the TBL fluid flow on the external side of the flexible wall, makes indispensable to express these energy functions in terms of concepts and formulations for random processes. Thus, a particular formulation is introduced in Section 1.6, which is inspired to a similar study proposed by (Gardonio et al. 2012) and refers to the formulations for stationary stochastic processes given in (Crandall and Mark 1963; Newland 1975; Bendat and Piersol 2000).