Growth rate of two-dimensional wake, using the general momentum integral equation

As explained the two boundary layers at the trailing edge of a body will join up and form a wake of retarded flow. The velocity profile across this wake will vary appreciably with distance behind the trailing edge. Some simple calculations can be made that will relate the rate of growth of the wake thickness to distance downstream, provided the wake profile shape and external mainstream conditions can be specified.

The momentum integral equation for steady incompressible flow, Eqn (7.98) may be reduced to

Now Cf is the local surface shear stress coefficient at the base of the boundary layer, and at the wake centre, where the two boundary layers join, there is no relative velocity and therefore no shearing traction. Thus, for each half of the wake, Q is zero and Eqn (7.171) becomes

It is clear from this that if the mainstream velocity outside the wake is constant, then dUe/dx = 0 and the right-hand side becomes zero, i. e. the momentum thickness of the wake is constant. This would be expected from the direct physical argument that there are no overall shearing tractions at the wake edges under these conditions, so that the total wake momentum will remain unaltered with distance downstream. 0 may represent the momentum thickness for each half of the wake, considered separately if it is unsymmetrical, or of the whole wake if it is symmetrical.

The general thickness S of the wake is then obtainable from the relationship

0 — S f m(1 — u) dy = IS Jo

so that

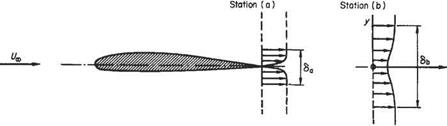
<5b _ Оъ h <5a 0a h

where suffices a and b refer to two streamwise stations in the wake. Knowledge of the velocity profiles at stations a and b is necessary before the integrals 7a and /ь can be evaluated and used in this equation.

Example 7.11 A two-dimensional symmetrical aerofoil model of 0.3 m chord with a roughened surface is immersed, at zero incidence, in a uniform airstream flowing at 30 m s_ 1. The minimum velocity in the wake at a station 2.4 m downstream from the trailing edge is 27 ms-1. Estimate the general thickness of the whole wake at this station. Assume that each boundary layer at the trailing edge has a ‘seventh root’ profile and a thickness corresponding to a turbulent flat-plate growth from a point at 10% chord, and that each half-wake profile at the downstream station may be represented by a cubic curve of the form U = ay? + by2 + cy + d.

At the trailing edge, where. v = 0.3 m:

(Eqn (7.81))

z Re Xі

Re[/S = 14.39

1 r 0.383 x 0.27 л „ 2^a = 14.39 =°-00719m

Also

/„ = 0.0973 Eqn (a) (Section 7.7.5)

At the wake station:

и = a у + bv + су + d, — = Ъаг + 2 by + c ■ ’ dy ■

The conditions to be satisfied are that (і) й = 0.9 and (ii) дй/ду = 0, when у = 0; and (iii) й = 1.0 and (iv) дй/ду = 0, when у = 1. (Condition (ii) follows because, once the wake is established at a short distance behind the trailing edge, the profile discontinuity at the centre­line disappears.) Thus:

a = lh

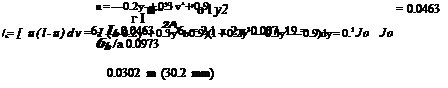= (1 — j + 0.9 or /> = 0.3 and a = -0.2