Horizontal Flight Endurance and Range
Horizontal flight endurance is the time in the course of which the helicopter can perform horizontal flight using the available fuel supply. Flight endurance is found from the formula
T = Gfuel
hr" %
where the fuel supply for horizontal flight, liters;
c^ is the fuel consumption per hour, liters/hr.
This formula shows that the endurance depends on the fuel supply and the hourly consumption. The fuel supply for horizontal flight is the
difference between the amount of fuel serviced into the tanks G and the amount of fuel expended in the other flight regimes: taxiing, takeoff, climb,
descent, and landing. The fuel consumption in these flight regimes is indicated in the instructions for calculating flight endurance and range, which are prepared for each helicopter type on the basis of calculations and flight tests.
![]()
The hourly fuel consumption is the amount of fuel which the engine consumes per hour of operation. It is found from the formula
= = <29)
where ce is the specific fuel consumption;
N is the effective engine power; e
C, is the power utilization coefficient.
Since c£ and £ change only slightly with variation of the flight speed, their ratio can be assumed constant and (29) takes the form
ch = const /Vh.
This formula shows that the hourly fuel consumption depends on the /99
power required for helicopter horizontal flight, and consequently, on the flight speed.
Using the curve of power versus speed (see Figure 62), we can say that the minimal power required for horizontal flight corresponds to the economical speed; therefore, the minimal hourly fuel consumption corresponds to this speed.
In order for the helicopter to stay in the air for the maximal time, flight must be performed at the economical speed. The economical speed depends on helicopter weight: this speed increases with increase of the weight, and
the flight endurance decreases. Since the economical speed changes very little with altitude, the horizontal flight endurance decreases somewhat with increase of the altitude as a result of the increased fuel consumption in climb and descent.
Helicopter horizontal flight range is the distance which the helicopter can fly while utilizing the fuel supply for horizontal flight
(ЗО)
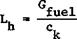 where is the fuel consumption per kilometer, liters/km.
where is the fuel consumption per kilometer, liters/km.
The horizontal flight range is larger, the larger the fuel supply and the lower the consumption per kilometer. The fuel supply is defined as in the flight endurance calculation. The consumption per kilometer is found from the formula
c* ^ if – = const ~r~.
The minimal fuel consumption per kilometer will be achieved with the
minimal ratio N, /V.
n
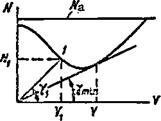
Let us examine the power required and available curves for horizontal flight (Figure 66). Any point on the power required curve corresponds to definite values of V and N. For example, the point 1 corresponds to the speed V^, and the power required N^. The ratio of these quantities is equal to tg Y, and therefore, the consumption per kilometer is
= const tg
This means that tg у must be minimal in order to obtain the minimal fuel consumption per kilometer. This corresponds to the angle between the tangent to the power required curve and the horizontal axis. The point of tangency will correspond to the optimal helicopter horizontal flight speed.
Thus, the maximal horizontal flight range is achieved at the optimal
speed, which corresponds to the minimal fuel consumption per kilometer only if the engine is carefully adjusted. In this case, the calculation of the maximal range is made using the fuel consumption per kilometer curves plotted
on the basis of experimental helicopter operational data. The speed obtained from these curves and the corresponding minimal consumption will be close to the optimal values.
![]()
 The consumption per kilometer is the fuel burned per kilometer of air distance (relative to the air). Consequently, the flight range calculation made using (30) is valid only if there is no wind. If there is wind, the
The consumption per kilometer is the fuel burned per kilometer of air distance (relative to the air). Consequently, the flight range calculation made using (30) is valid only if there is no wind. If there is wind, the
flight range will vary, depending on the wind direction and velocity. The so – called navigational fuel supply, amounting to 10-15% of the required fuel, is set aside as reserve in case the weather conditions change. Since the power required for horizontal flight depends on helicopter weight and flight altitude, the fuel consumption per kilometer increases, and the range decreases with increase of the weight. The average flight weight is used for exact range calculations
|
|
where G is the takeoff weight;
Gf і is the fuel supply for horizontal flight.
With increase of the altitude the optimal speed increases somewhat, and the power required decreases, therefore, the fuel consumption per kilometer also decreases. But the climb to a higher altitude requires more fuel. In practice, the longest flight range without account for wind is obtained at an altitude from 1000 to 2000 meters. For the Mi-1, the minimal fuel consumption per kilometer is 0.56 liters/km at an altitude of 1000 meters and an indicated airspeed of 130 km/hr. The flight range with this fuel consumption rate is 370 km.














